Trong mặt phẳng toạ độ, cho điểm H có toạ độ (3;2). Hãy vẽ điểm K đới xứng với H qua gốc toạ độ và tìm toạ độ của K
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
29 tháng 9 2023
a) Khoảng cách từ gốc tọa độ \(O\left( {0;0} \right)\) đến điểm \(M\left( {3;4} \right)\) trong mặt phẳng tọa độ Oxy là:
\(OM = \left| {\overrightarrow {OM} } \right| = \sqrt {{3^2} + {4^2}} = 5\)
b) Với hai điểm I(a; b) và M(x ; y) trong mặt phẳng toạ độ Oxy, ta có:\(IM = \sqrt {{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2}} \)
HQ
Hà Quang Minh
Giáo viên
28 tháng 9 2023
a) Dựa vào hình vẽ ta thấy \(A\left( {1; - 3} \right)\)
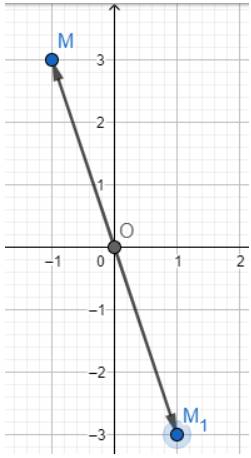
b) Dựa vào hình vẽ ta thấy \(B\left( { - 1; - 3} \right)\)
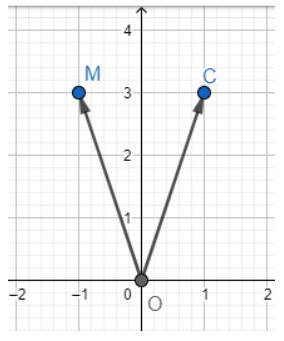
c) Dựa vào hình vẽ ta thấy \(C\left( {1;3} \right)\)
SG
30 tháng 4 2023
a, (d) cắt trục hoành tại A(xA;0) và trục tung B(0;xB)
Vì A thuộc (d) nên \(0=-2x_A+4\Leftrightarrow x_A=2 \Rightarrow A(2;0)\)
Vì B thuộc (d) nên \(y_B=-2.0+4=4\Rightarrow B(0;4)\)
Vậy A(2;0) và B(0;4) là hai điểm cần tìm.
b, Gọi C(xc;yc) là điểm có hoành độ bằng tung độ
⇒ xc = yc = a. Vì C thuộc (d) nên \(a=-2a+4\Leftrightarrow a=\dfrac{4}{3}\)
⇒ \(C(\dfrac{4}{3};\dfrac{4}{3})\) là điểm cần tìm.
CM
27 tháng 3 2018
Đáp án A.
Gọi:
Phương trình mặt phẳng (P) có dạng:
Vì M là trực tâm của tam giác ABC nên
CM
30 tháng 4 2019
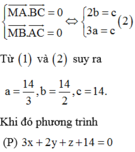
Đáp án B
Phương trình mặt phẳng (Oyz) là x=0 và hình chiếu của điểm I(a;b;c) lên mặt phẳng (Oyz) là (0;b;c).
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 1 2024
a.
Gọi \(D\left(x;y\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-5;-1\right)\\\overrightarrow{DC}=\left(3-x;-2-y\right)\end{matrix}\right.\)
Do ABCD là hình bình hành \(\Rightarrow\overrightarrow{AB}=\overrightarrow{DC}\)
\(\Rightarrow\left\{{}\begin{matrix}3-x=-5\\-2-y=-1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=8\\y=-1\end{matrix}\right.\)
\(\Rightarrow D\left(8;-1\right)\)
Gọi O là tâm hình bình hành \(\Rightarrow\) O là trung điểm AC
Theo công thúc trung điểm:
\(\left\{{}\begin{matrix}x_O=\dfrac{x_A+x_C}{2}=\dfrac{7}{2}\\y_O=\dfrac{y_A+y_C}{2}=\dfrac{1}{2}\end{matrix}\right.\) \(\Rightarrow O\left(\dfrac{7}{2};\dfrac{1}{2}\right)\)
b.
Theo công thức trọng tâm: \(\left\{{}\begin{matrix}x_G=\dfrac{x_A+x_B+x_C}{3}=2\\y_G=\dfrac{y_A+y_B+y_C}{3}=1\end{matrix}\right.\)
\(\Rightarrow G\left(2;1\right)\)
I đối xứng B qua G \(\Rightarrow G\) là trung điểm IB
\(\Rightarrow\left\{{}\begin{matrix}x_I=2x_G-x_B=5\\y_I=2y_G-y_B=0\end{matrix}\right.\) \(\Rightarrow I\left(5;0\right)\)
\(\left\{{}\begin{matrix}\dfrac{x_A+x_D+x_C}{3}=5=x_I\\\dfrac{y_A+y_D+y_C}{3}=0=y_I\end{matrix}\right.\) \(\Rightarrow I\) là trọng tâm ADC
c.
Ta có: \(S_{ABC}=\dfrac{1}{2}AB.d\left(C;AB\right)\)
\(S_{ABM}=\dfrac{1}{2}AB.d\left(M;AB\right)\)
\(S_{ABC}=3S_{ABM}\Rightarrow d\left(C;AB\right)=3d\left(M;AB\right)\)
\(\Rightarrow BM=\dfrac{1}{3}BC\)
\(\Rightarrow\left[{}\begin{matrix}\overrightarrow{BM}=\dfrac{1}{3}\overrightarrow{BC}\\\overrightarrow{BM}=-\dfrac{1}{3}\overrightarrow{BC}\end{matrix}\right.\)
Gọi \(M\left(x;y\right)\Rightarrow\overrightarrow{BM}=\left(x+1;y-2\right)\)
\(\Rightarrow\left[{}\begin{matrix}\left(x+1;y-2\right)=\dfrac{1}{3}\left(4;-4\right)\\\left(x+1;y-2\right)=-\dfrac{1}{3}\left(4;-4\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\left(x;y\right)=\left(\dfrac{1}{3};\dfrac{2}{3}\right)\\\left(x;y\right)=\left(-\dfrac{7}{3};\dfrac{10}{3}\right)\end{matrix}\right.\)