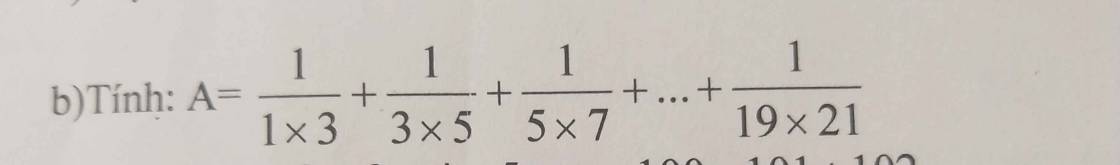Giải nhanh giúp tớ với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(PTK_x=2\cdot56+\left(32+16\cdot4\right)a=400\\ \Rightarrow96a=288\\ \Rightarrow a=3\)
Do đó CTHH \(X:Fe_2\left(SO_4\right)_3\)
Vì \(SO_4\left(II\right)\Rightarrow Fe\left(III\right)\)

\(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}\)
\(=\frac{16}{32}+\frac{8}{32}+\frac{4}{32}+\frac{2}{32}+\frac{1}{32}\)
\(=\frac{31}{32}\)

Ta có: \(n_{CH_3COOH}=\dfrac{60}{60}=1\left(mol\right)\)
a, PT: \(2CH_3COOH+K_2CO_3\rightarrow2CH_3COOK+CO_2+H_2O\)
_________1____________________1_________0,5 (mol)
b, VCO2 = 0,5.22,4 = 11,2 (l)
c, mCH3COOK = 1.98 = 98 (g)
Bạn tham khảo nhé!
a) PTHH: 2CH3COOH + K2CO3 → 2CH3COOK + CO2↑ + H2O
b) nCH3COOH = \(\dfrac{m}{M}=\dfrac{60}{60}=1\left(mol\right)\)
Theo PTHH: nCO2 = \(\dfrac{1}{2}\).nCH3COOH = 0,5 (mol)
=> VCO2 (đktc) = n.22,4 = 0,5.22,4 = 11,2 (lít)
c) Theo PTHH: nCH3COOK = nCH3COOH = 1 (mol)
=> mCH3COOK = n.M = 1.98 = 98 (g)
Mặc dù hơi muộn nhưng mà chúc bạn thi đạt kết quả tốt nha ^_^

\(5^{11}và7^7=\left(5.7\right)^4và\left(7.5\right)^2=35^4>35^2\)

a: Bảng tần số:
| Thời gian | 15 | 17 | 18 | 19 | 20 | 23 |
| Tần số | 1 | 3 | 2 | 1 | 6 | 5 |
Lớp 8A có 18 bạn nam
Mốt của dấu hiệu là 20
b: thời gian trung bình là;
\(\dfrac{15\cdot1+17\cdot3+18\cdot2+19\cdot1+20\cdot6+23\cdot5}{18}\simeq19,78\)
d: Thời gian chạy của bạn đó là;
20*19-19,78*18=23,96(giây)

\(=\left(\dfrac{\sqrt{5}\left(\sqrt{3}-2\right)}{\sqrt{3}-2}+\dfrac{\sqrt{6}\left(\sqrt{3}+\sqrt{2}\right)}{\sqrt{3}+\sqrt{2}}-\dfrac{\sqrt{6}-\sqrt{5}}{\left(\sqrt{6}-\sqrt{5}\right)\left(\sqrt{6}+\sqrt{5}\right)}\right):\sqrt{\dfrac{5}{2}}\)
\(=\left(\sqrt{5}+\sqrt{6}-\sqrt{6}+\sqrt{5}\right):\dfrac{\sqrt{5}}{\sqrt{2}}\)
\(=2\sqrt{5}.\dfrac{\sqrt{2}}{\sqrt{5}}=2\sqrt{2}\)
a) Ta có: \(\left(\dfrac{\sqrt{15}-\sqrt{20}}{\sqrt{3}-2}+\dfrac{3\sqrt{2}+2\sqrt{3}}{\sqrt{3}+\sqrt{2}}-\dfrac{1}{\sqrt{6}+\sqrt{5}}\right):\sqrt{\dfrac{5}{2}}\)
\(=\left(\sqrt{5}+\sqrt{6}-\sqrt{6}+\sqrt{5}\right):\dfrac{\sqrt{10}}{2}\)
\(=2\sqrt{5}\cdot\dfrac{2}{\sqrt{10}}=2\sqrt{2}\)

`#040911`
`b)`
\(A=\dfrac{1}{1\times3}+\dfrac{1}{3\times5}+\dfrac{1}{5\times7}+...+\dfrac{1}{19\times21}\)
`=`\(\dfrac{1}{2}\times\left(\dfrac{2}{1\times3}+\dfrac{2}{3\times5}+\dfrac{2}{5\times7}+...+\dfrac{2}{19\times21}\right)\)
`=`\(\dfrac{1}{2}\times\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{19}-\dfrac{1}{21}\right)\)
`=`\(\dfrac{1}{2}\times\left(1-\dfrac{1}{21}\right)\)
\(=\dfrac{1}{2}\times\dfrac{20}{21}\\ =\dfrac{10}{21}\\ \text{ Vậy, A = }\dfrac{10}{21}\)

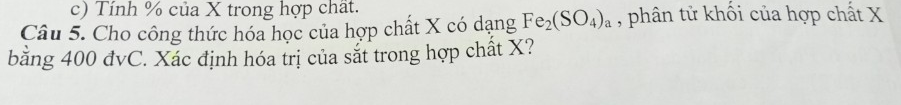

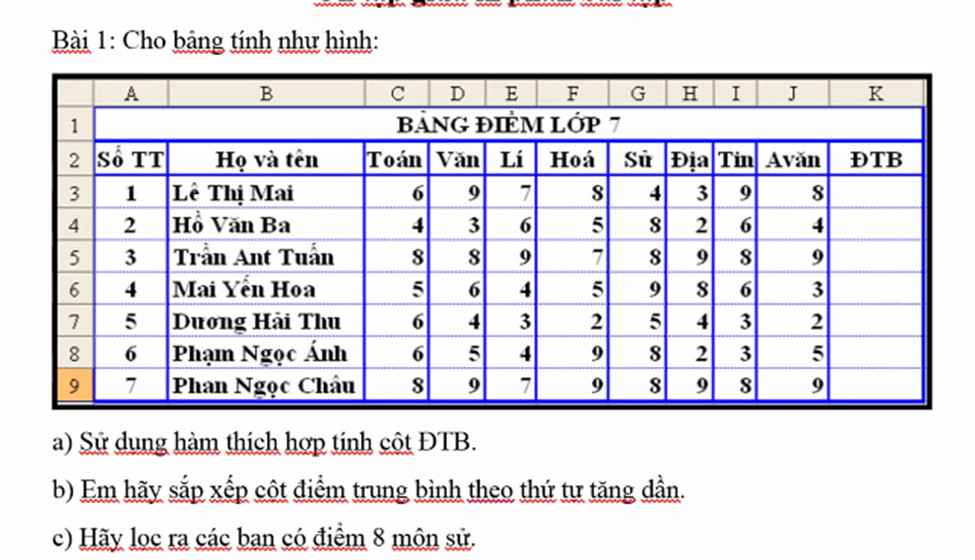

 Giải giúp tớ với ạ, tớ cần gấp lắm
Giải giúp tớ với ạ, tớ cần gấp lắm