Giải giúp em câu 3.4.5.6.7
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H9
HT.Phong (9A5)
CTVHS
27 tháng 8 2023
a) Xét 1976:
Ta có 1976 chia hết cho 2 không chia hết cho 3;5;9
Và: 380 chia hết cho 2;5
Vậy tổng trên chia hết cho 2
b) Xét 2415
Ta có 2415 chia hết cho 3; 5
Và: 780 chia hết cho 2;5;3
Vậy hiệu trên chia hết cho 3 và 5
c) Xét 2.4.6.8:
Ta có: 2.4.6.8 chia hết cho 2; 3
Và: 14 chia hết cho 2
Vậy tổng trên chia hết cho 2
d) Xét 3.4.5.6.7:
Ta có: 3.4.5.6.7 chia hết cho 2;3;5;9
Và: 45 chia hết cho 3;9;5
Vậy hiệu trên chia hết cho 3;9 và 5
TP
27 tháng 8 2023
a) Tổng của 1976 và 380 là 1976+380=2356. Số này chia hết cho 2 vì chữ số cuối cùng là 6. Số này không chia hết cho 3 vì tổng các chữ số của nó là 2+3+5+6=16 không chia hết cho 3. Số này không chia hết cho 5 vì chữ số cuối cùng không phải là 0 hoặc 5. Số này không chia hết cho 9 vì tổng các chữ số của nó không chia hết cho 9.
b) Hiệu của 2415 và 780 là 2415−780=1635. Số này chia hết cho 3 vì tổng các chữ số của nó là 1+6+3+5=15 chia hết cho 3. Số này không chia hết cho 2 vì chữ số cuối cùng là 5. Số này chia hết cho 5 vì chữ số cuối cùng là 5. Số này không chia hết cho 9 vì tổng các chữ số của nó không chia hết cho 9.
c) Tổng của các số trong biểu thức 2.4.6.8+14 là 2+4+6+8+14=34. Số này không chia hết cho bất kỳ số nào trong danh sách {2,3,5,9}.
d) Hiệu của các số trong biểu thức 3.4.5.6.7−45 là 3+4+5+6+7−45=−20. Số này chỉ chia hết cho số trong danh sách {2,3,5,9} là số -20.
NN
1
6 tháng 12 2021
a,
c, Gọi \(\left(D_3\right):y=ax+b\) là đt cần tìm
\(\Leftrightarrow\left\{{}\begin{matrix}a=-2;b\ne0\\3x+3=ax+b,\forall x=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-2\\-a+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b=-2\end{matrix}\right.\)
Vậy \(\left(D_3\right):y=-2x-2\)
L
0
VD
11 tháng 1 2021
Gọi giao điểm AE và BP là F;
Gọi giao điểm QD và AB là H;
Gọi kéo dài AD cắt BF tại P'
Dễ cm M là trung điểm AC
Xét \(\Delta OMC\) có QD//CM\(\Rightarrow\dfrac{OD}{OM}=\dfrac{QD}{CM}\)(hệ quả tales)
Tương tự với \(\Delta OAM\) có \(\dfrac{OD}{OM}=\dfrac{DH}{AM}\)
\(\Rightarrow\dfrac{QD}{CM}=\dfrac{DH}{AM}\)
Mà CM=AM (vì M là tđ AC)
\(\Rightarrow QD=DH\)
Dễ cm P là trung điểm BF
Xét \(\Delta ABP'\) có DH//BP'
\(\Rightarrow\dfrac{DH}{BP'}=\dfrac{AD}{AP'}\)(tales)
Tương tự với \(\Delta AFP'\) có \(\dfrac{QD}{FP'}=\dfrac{AD}{AP'}\)
\(\Rightarrow\dfrac{DH}{BP'}=\dfrac{QD}{FP'}\)
Mà DH=QD (cmt)
\(\Rightarrow BP'=FP'\)
\(\Rightarrow\)P' là trung điểm BF
\(\Rightarrow P\equiv P'\)
\(\Rightarrow A,D,P\) thẳng hàng
20 tháng 6 2016
( 3.4.5.6.7 ) + ( x.24 )
= 2520 + 24x
= 105.24 + 24.x
= 24 ( 105 + x )
NT
5
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 10 2021
b.
\(\Leftrightarrow\dfrac{1}{2}cosx-\dfrac{\sqrt{3}}{2}sinx=-\dfrac{1}{2}\)
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{3}\right)=-\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{3}=\dfrac{2\pi}{3}+k2\pi\\x+\dfrac{\pi}{3}=-\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k2\pi\\x=-\pi+k2\pi\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 10 2021
c.
\(\Leftrightarrow\dfrac{3}{5}sinx-\dfrac{4}{5}cosx=1\)
Đặt \(\dfrac{3}{5}=cosa\) với \(a\in\left(0;\dfrac{\pi}{2}\right)\Rightarrow\dfrac{4}{5}=sina\)
Pt trở thành:
\(sinx.cosa-cosx.sina=1\)
\(\Leftrightarrow sin\left(x-a\right)=1\)
\(\Leftrightarrow x-a=\dfrac{\pi}{2}+k2\pi\)
\(\Leftrightarrow x=a+\dfrac{\pi}{2}+k2\pi\)
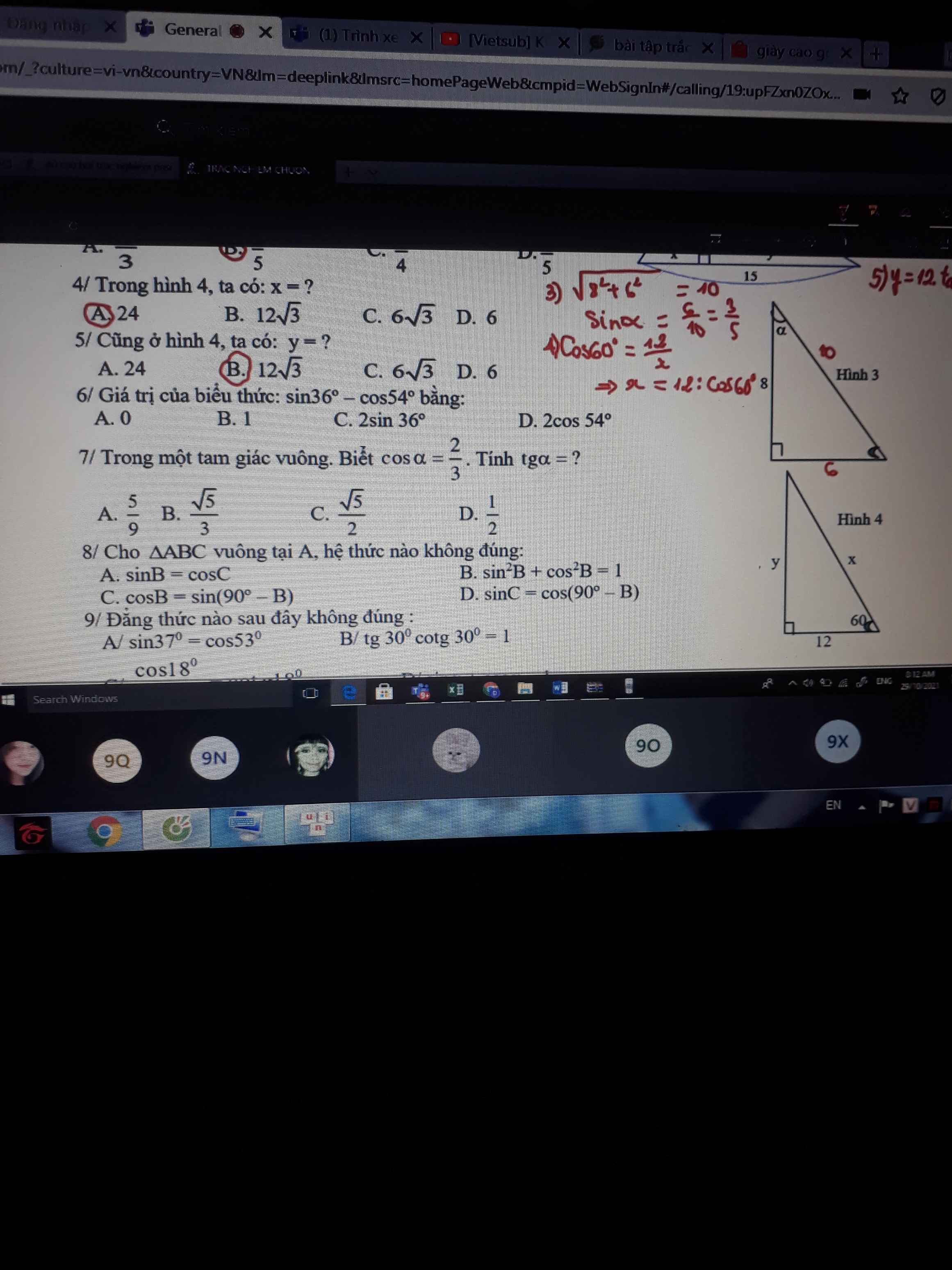
câu 3
\(n_{H_2}=\dfrac{2,24}{22,4}=0,1\left(mol\right)\\ pthh:Fe+2HCl\rightarrow FeCl_2+H_2\uparrow\)
0,1 0,2 0,1
\(m_{Fe}=0,1.56=5,6g\\ V_{HCl}=0,2:2=0,1\left(mol\right)\)