Áp dụng cái gì ra vậy mí bạn? x1² +x2² - x1x2 = (x1 + x2)2 - 3x1x2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{3}{2}\\x_1x_2=-\dfrac{1}{2}\end{matrix}\right.\)
\(A=\dfrac{1}{x_1-3}+\dfrac{1}{x_2-3}=\dfrac{x_2-3+x_1-3}{\left(x_1-3\right)\left(x_2-3\right)}=\dfrac{x_1+x_2-6}{x_1x_2-3\left(x_1+x_2\right)+9}\)
\(=\dfrac{\dfrac{3}{2}-6}{-\dfrac{1}{2}-3.\dfrac{3}{2}+9}=...\) (em tự bấm máy)
\(B=x_1^2x_2-4-x_1x_2+x_1x_2^2=x_1x_2\left(x_1+x_2\right)-4-x_1x_2\)
\(=-\dfrac{1}{2}.\dfrac{3}{2}-4-\left(-\dfrac{1}{2}\right)=...\)
\(C=1-\left(x_1^2+x_2^2\right)=1-\left(x_1+x_2\right)^2+2x_1x_2=1-\left(\dfrac{3}{2}\right)^2+2.\left(-\dfrac{1}{2}\right)=...\)
\(D=x_1^3x_2^3+x_1^3+x_2^3=\left(x_1x_2\right)^3+\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)\)
\(=\left(-\dfrac{1}{2}\right)^3+\left(\dfrac{3}{2}\right)^3-3.\left(-\dfrac{1}{2}\right).\dfrac{3}{2}=...\)

\(2x^2-6x-3=0\)
\(\Delta'=\left(-3\right)^2+3.2=15>0\)
⇒ Phương trình có hai nghiệm phân biệt với mọi m.
Theo hệ thức viét ta có : \(\left\{{}\begin{matrix}x_1+x_2=3\\x_1.x_2=-\dfrac{3}{2}\end{matrix}\right.\)
Ta có : \(B=3x_1x_2-x_1^2-x_2^2=-\left(x_1+x_2\right)^2+5x_1x_2=-9+5.\left(-\dfrac{3}{2}\right)=\dfrac{135}{2}\)
Vậy \(B=-\dfrac{135}{2}\) với hai nghiệm phân biệt thỏa mãn.

\(\Delta'=m^2-\left(2m^2-4m+3\right)=-m^2+4m-3\)
\(=-\left(m^2-4m+4-4\right)-3=-\left(m-2\right)^2+1\)
Để pt trên có 2 nghiệm x1 ; x2 khi \(0\le-\left(m-2\right)^2+1\le1\)
Theo Vi et : \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=2m^2-4m+3\end{matrix}\right.\)
\(A=\left(x_1+x_2\right)^2+x_1x_2\)
\(=4m^2+2m^2-4m+3=6m^2-4m+4\)
bạn kiểm tra lại đề xem có vấn đề gì ko ?
\(\Delta'=m^2-\left(2m^2-4m+3\right)=-m^2+4m-3\ge0\Rightarrow1\le m\le3\)
Theo Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=2m^2-4m+3\end{matrix}\right.\)
\(A=\left(x_1+x_2\right)^2+x_1x_2\)
\(=\left(2m\right)^2+2m^2-4m+3\)
\(=6m^2-4m+3\)
Xét hàm \(f\left(m\right)=6m^2-4m+3\) trên \(\left[1;3\right]\)
\(-\dfrac{b}{2a}=\dfrac{1}{3}< 1;a=6>0\Rightarrow f\left(m\right)\) đồng biến trên \(\left[1;3\right]\)
\(\Rightarrow f\left(m\right)_{max}=f\left(3\right)=45\) khi \(m=3\)

Phương trình x 2 – 2(m + 4)x + m 2 – 8 = 0 có a = 1 ≠ 0 và
∆ ' = ( m + 4 ) 2 – ( m 2 – 8 ) = 8 m + 24
Phương trình có hai x 1 ; x 2 ⇔ ∆ ' ≥ 0 ⇔ 8 m + 24 ≥ 0
Áp dụng định lý Vi – ét ta có x 1 + x 2 = 2 ( m + 4 ) ; x 1 . x 2 = m 2 – 8
Ta có:
A = x 1 + x 2 − 3 x 1 x 2
= 2 (m + 4) – 3 ( m 2 – 8) = 3 m 2 + 2m + 32 = − 3 m 2 − 2 3 m − 32 3
= − 3 m − 1 3 2 + 97 3
Nhận thấy A ≤ 97 3 và dấu “=” xảy ra khi m − 1 3 = 0 ⇔ m = 1 3 (TM)
Vậy giá trị lớn nhất của A là 97 3 khi m = 1 3
Đáp án: A

\(\Delta'=\left(m+1\right)^2-\left(5m+1\right)=m^2-3m\ge0\Rightarrow\left[{}\begin{matrix}m\ge3\\m\le0\end{matrix}\right.\)
\(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)\\x_1x_2=5m+1\end{matrix}\right.\)
a.
\(S=\left(x_1+x_2\right)^2-3x_1x_2=4\left(m+1\right)^2-3\left(5m+1\right)\)
\(=4m^2-7m+1=\dfrac{7}{3}\left(m^2-3m\right)+\dfrac{5}{3}m^2+1\ge1\)
\(S_{min}=1\) khi \(\dfrac{7}{3}\left(m^2-3m\right)+\dfrac{5}{3}m^2=0\Rightarrow m=0\)
b.
\(1< x_1< x_2\Rightarrow\left\{{}\begin{matrix}\left(x_1-1\right)\left(x_2-1\right)>0\\\dfrac{x_1+x_2}{2}>1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x_1x_2-\left(x_1+x_2\right)+1>0\\x_1+x_2>2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}5m+1-2\left(m+1\right)+1>0\\2\left(m+1\right)>0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m>0\\m>-1\end{matrix}\right.\) \(\Rightarrow m>0\)
Kết hợp điều kiện delta \(\Rightarrow m\ge3\)
\(a,\Leftrightarrow\Delta\ge0\Leftrightarrow\left(2m+2\right)^2-4\left(5m+1\right)\ge0\Leftrightarrow4m^2-12m\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}m\le0\\m\ge3\end{matrix}\right.\)
\(vi-ét\Rightarrow\left\{{}\begin{matrix}x1+x2=2m+2\\x1x2=5m+1\end{matrix}\right.\)
\(\Rightarrow S=x1^2+x2^2-x1x2=\left(x1+x2\right)^2-3x1x2\)
\(=\left(2m+2\right)^2-3\left(5m+1\right)=4m^2-7m+1\)
\(=\left(2m\right)^2-2.2.\dfrac{7}{4}.m+\left(\dfrac{7}{4}\right)^2-\dfrac{33}{16}=\left(2m-\dfrac{7}{4}\right)^2-\dfrac{33}{16}\left(1\right)\)
\(TH1:m\ge3\Rightarrow\left(1\right)\ge\left(2.3-\dfrac{7}{4}\right)^2-\dfrac{33}{16}=16\)
\(TH2:m\le0\Rightarrow\left(1\right)\ge\left(0-\dfrac{7}{4}\right)^2-\dfrac{33}{16}=1\)
\(\Rightarrow MinS=1\Leftrightarrow m=0\left(tm\right)\)
\(b,1< x1< x2\Leftrightarrow0< x1-1< x2-1\)
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta>0\\\left(x1-1\right)\left(x2-1\right)>0\\x1+x2-2>0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m>3\\m< 0\end{matrix}\right.\\\left[{}\begin{matrix}\left\{{}\begin{matrix}x1>1\\x2>1\end{matrix}\right.\\\left\{{}\begin{matrix}x1 < 1\\x2< 1\end{matrix}\right.\end{matrix}\right.\\2m+2-2>0\\\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m>3\\m< 0\end{matrix}\right.\\\left[{}\begin{matrix}x1x2>1\\x1x2< 1\end{matrix}\right.\\m>0\\\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m>3\\m< 0\end{matrix}\right.\\\left[{}\begin{matrix}m>0\\m< 0\end{matrix}\right.\\m>0\\\end{matrix}\right.\Rightarrow m>3\)
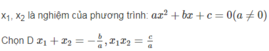

x12 +x22= (x12 + 2x1x2 + x22) - 2x1x2 (*vì cộng 2x1x2 rồi nên -2x1x2 để cân bằng tỉ số)
Ở đây ta thấy biểu thức trong ngoặc là hẳng đẳng thức => (x1 +x2)2 - 2x1x2 - x1x2 = (x1 +x2)2 - 3x1x2