Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
xét tam giác ABC và tam giác HBA có
góc BAC=góc AHB=90 độ
góc B chung
suy ra tam giác ABC đồng dạng với tam giác HBA
suy ra AB phần HB = BC phần AB
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
\(BC=\sqrt{9^2+12^2}=15\left(cm\right)\)
AH=9*12/15=7,2cm
b: ΔHAB vuông tại H có HM vuông góc AB
nên MH^2=MA*MB
tự kẻ hình
a, xét tam giác ABC và tam giác HBA có : góc B chung
góc BAC = góc BHA = 90
=> tam giác ABC đồng dạng với tam giác HBA (g-g)
=> AB/BH = AC/AH
=> AB.AH = BH.AC
b, xét tam giác BAH vuông tại H => HB^2 + HA^2 = AB^2 (Pytago)
BH = 3; AB = 5(gt)
=> 3^2 + AH^2 = 5^2
=> AH^2 = 16
=> AH = 4 do AH > 0
xét tam giác ABH có : BI là pg của góc ABH (gt)
=> AI/AB = IH/BH (tính chất)
=> AI+IH/AB+BH = AI/AB = IH/BH
=> AH/AB + BH = AI/AB = IH/BH
có: AH = 4; AB = 5; BH = 3
=> 4/3+5 = AI/5 = IH/3
=> AI/5 = IH/3 = 1/2
=> AI = 5/2 và IH = 3/2
c, góc CAH = 90 - góc HAB
góc HBA = 90 - góc HAB
=> góc CAH = góc HBA
xét tam giác AHC và tam giác BHA có: góc AHC = góc BHA = 90
=> tam giác AHC đồng dạng với tam giác BHA (g-g)
=> AC/AB = AH/HB
=> AC/AH = AB/HB
BI là pg của tam giác AHB => AI/AH = AB/AB
CK là pg của tam giác AHC => CK/KH = AC/AH
=> AI/AH = CK/KH
=> KI // AC
a:
Ta có: DE\(\perp\)AC
AB\(\perp\)AC
Do đó: DE//AB
Xét ΔCAB có ED//AB
nên \(\dfrac{CE}{EA}=\dfrac{CD}{DB}\)
=>\(\dfrac{BD}{DC}=\dfrac{AE}{EC}\)
b: Xét ΔHBA vuông tại H và ΔEDC vuông tại E có
\(\widehat{EDC}=\widehat{HBA}\)(hai góc đồng vị, DE//AB)
Do đó: ΔHBA~ΔEDC
a, Xét tam giác ABC và tam giác HBA ta có :
^BAC = ^AHB = 900
^B _ chung
Vậy tam giác ABC ~ tam giác HBA ( g.g )
c, tam giác ABC vuông tại A, có đường cao AH
Áp dụng định lí Pytago cho tam giác ABC vuông tại A
\(AB^2+AC^2=BC^2\Rightarrow BC^2=36+64=100\Rightarrow BC=10\)cm
Ta có : \(\dfrac{AC}{AH}=\dfrac{BC}{AB}\)( cặp tỉ số đồng dạng ý a )
\(\Rightarrow\dfrac{8}{AH}=\dfrac{10}{6}\Rightarrow AH=\dfrac{48}{10}=\dfrac{24}{5}\)cm
d, phải là cắt AC nhé, xem lại đề nhé bạn
a) Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{B}\) chung
Do đó: ΔABC\(\sim\)ΔHBA(g-g)
a) Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABH}\) chung
Do đó: ΔABC\(\sim\)ΔHBA(g-g)
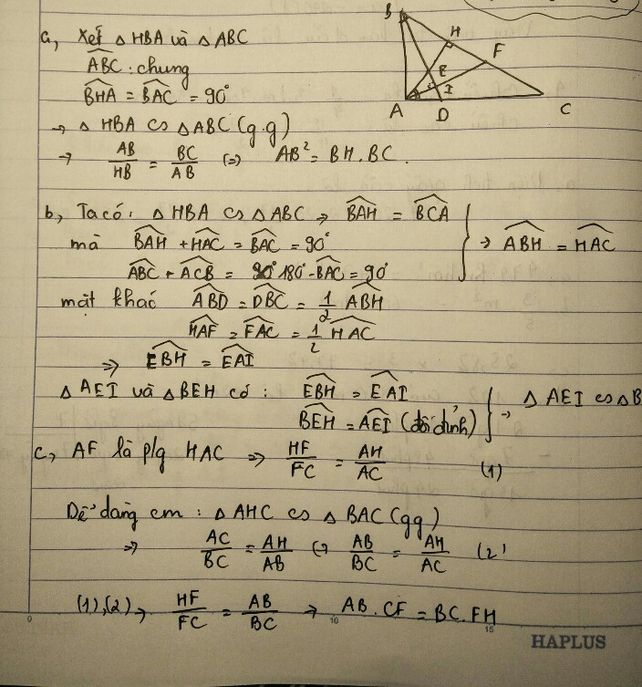
a/
Xét tg vuông ABC và tg vuông HBA có \(\widehat{ACB}=\widehat{HAB}\) (cùng phụ với \(\widehat{ABC}\) )
=> tg ABC đồng dạng với tg HBA (g.g.g)
b/
\(BC=\sqrt{AB^2+AC^2}=\sqrt{9^2+12^2}=5\sqrt{5}\) (Pitago)
\(AB^2=BH.BC\) (trong tg vuông bình phương 1 cạnh góc vuông băng tích giữa hình chiếu của cạnh góc vuông đó trên cạnh huyền với cạnh huyền)
\(\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{81}{5\sqrt{5}}=\dfrac{81\sqrt{5}}{25}\)
\(\Rightarrow CH=BC-BH=5\sqrt{5}-\dfrac{81\sqrt{5}}{25}=\dfrac{44\sqrt{5}}{25}\)
Ta có
\(AH^2=BH.CH\) (trong tg vuông bình phường đường cao thuộc cạnh huyền băng tích giữa 2 hình chiếu của 2 cạnh góc vuông trên cạnh huyền)
\(\Rightarrow AH^2=\dfrac{81\sqrt{5}}{25}.\dfrac{44\sqrt{5}}{25}\) Khai căn ra AH
c/
Xét tg vuông BHI và tg vuông BEC có \(\widehat{CBE}\) chung
=> tg BHI đồng dạng với tg BEC (g.g.g)
\(\Rightarrow\dfrac{BI}{BC}=\dfrac{BH}{BE}\Rightarrow BI.BE=BH.BC\left(dpcm\right)\)