Bài 14. Cho △ABC cân tại A. Trên cạnh AB lấy điểm D, trên tia đối của tia CA lấy điểm E sao cho BD = CE. Gọi I là giao điểm của BC và DE.
a) Chứng minh : I là trung điểm của DE.
b) Gọi O là giao điểm của hai đường trung trực BC và DE. Chứng minh : △OBD = △OCE.
c) Chứng minh : OC vuông góc với AE.
Ơ....ơ... Gợi ý thui không cần giải ( có vẽ thêm không)

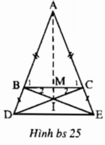
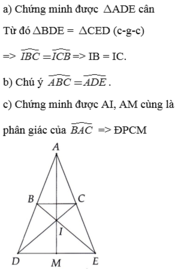
a: Kẻ DK//AC
=>góc DKB=góc ACB
=>góc DKB=góc DBK
=>DB=DK=CE
Xét tứ giác DKEC có
DK//EC
DK=EC
=>DKEC là hình bình hành
=>DE cắt KC tại trung điểm của mỗi đường
=>I là trung điểm của DE
b: O nằm trên trung trực của BC và DE
=>OB=OC; OD=OE
Xét ΔOBD và ΔOCE có
OB=OC
OD=OE
BD=CE
=>ΔOBD=ΔOCE