5.2x + 2x+2=288
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
2
8 tháng 8 2021
\(1,x^3-3x^2=0\)
\(x^2\left(x-3\right)=0\)
\(\orbr{\begin{cases}x^2=0\\x-3=0\end{cases}\orbr{\begin{cases}x=0\left(TM\right)\\x=3\left(TM\right)\end{cases}}}\)
\(2,3x^3-48x=0\)
\(3x\left(x^2-16\right)=0\)
\(\orbr{\begin{cases}3x=0\\x^2-16=0\end{cases}\orbr{\begin{cases}x=0\left(TM\right)\\x^2=16\end{cases}\orbr{\begin{cases}x=0\left(TM\right)\\x=\pm4\left(TM\right)\end{cases}}}}\)
\(3,5x\left(x-1\right)=x-1\)
\(5x^2-5x=x-1\)
\(5x^2-6x+1=0\)
\(5x^2-5x-x+1=0\)
\(5x\left(x-1\right)-\left(x-1\right)=0\)
\(\left(5x-1\right)\left(x-1\right)=0\)
\(\orbr{\begin{cases}5x-1=0\\x-1=0\end{cases}\orbr{\begin{cases}x=\frac{1}{5}\left(TM\right)\\x=1\left(TM\right)\end{cases}}}\)
\(4,2\left(x+5\right)-x^2-5x=0\)
\(2x+10-x^2-5x=0\)
\(-x^2-3x+10=0\)
\(-x^2-5x+2x+10=0\)
\(-x\left(x+5\right)+2\left(x+5\right)=0\)
\(\left(x+5\right)\left(2-x\right)=0\)
\(\orbr{\begin{cases}x+5=0\\2-x=0\end{cases}\orbr{\begin{cases}x=-5\left(TM\right)\\x=2\left(TM\right)\end{cases}}}\)
\(5,2x\left(x-5\right)-x\left(3+2x\right)=26\)
\(2x^2-10x-3x-2x^2=26\)
\(-13x-26=0\)
\(-13\left(x+2\right)=0\)
\(x=-2\left(TM\right)\)
QA
8 tháng 8 2021
Trả lời:
1, \(x^3-3x^2=0\)
\(\Leftrightarrow x^2\left(x-3\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x^2=0\\x-3=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=0\\x=3\end{cases}}}\)
Vậy x = 0; x = 3 là nghiệm của pt.
2, \(3x^3-48x=0\)
\(\Leftrightarrow3x\left(x^2-16\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}3x=0\\x^2-16=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=0\\x=\pm4\end{cases}}}\)
Vậy x = 0; x = 4; x = - 4 là nghiệm của pt.
3, \(5x\left(x-1\right)=x-1\)
\(\Leftrightarrow5x\left(x-1\right)-\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(5x-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-1=0\\5x-1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=1\\x=\frac{1}{5}\end{cases}}}\)
Vậy x = 1; x = 1/5 là nghiệm của pt.
4, \(2\left(x+5\right)-x^2-5x=0\)
\(\Leftrightarrow2\left(x+5\right)-x\left(x+5\right)=0\)
\(\Leftrightarrow\left(x+5\right)\left(2-x\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+5=0\\2-x=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-5\\x=2\end{cases}}}\)
Vậy x = - 5; x = 2 là nghiệm của pt.
5, \(2x\left(x-5\right)-x\left(3+2x\right)=26\)
\(\Leftrightarrow2x^2-10x-3x-2x^2=26\)
\(\Leftrightarrow-13x=26\)
\(\Leftrightarrow x=-2\)
Vậy x = - 2 là nghiệm của pt.
N
7 tháng 6 2017
x+2-3.4:5=2+4-5.2x
<=> x+2-12/5 = 6 - 10x
<=> 11x =6 - 2 + 12/5
<=> 11x = 32/5
<=> x = 32/55
k mik nha. tks bạn
7 tháng 6 2017
\(x+2-3.4:5=2+4-5.2x\)
=) \(x+2-\frac{12}{5}=6-10x\)
=) \(x+10x-\frac{12}{5}=6-2\)(CHUYỂN VẾ)
=) \(11x-\frac{12}{5}=4\)
=) \(11x=4+\frac{12}{5}=\frac{32}{5}\)
=) \(x=\frac{32}{5}:11=\frac{32}{55}\)
8 tháng 8 2023
4. ( x - 250 ) : 6 = 64 - 12
( x- 250 ) : 6 = 52
x - 250 = 312
x = 562
5. 10x = 1030
=> x = 103
6. 30x = 120
x = 4
7. \(x=2023\)
\(8.165-\left(35:x+3\right).19=13\)
\(\left(35:x+3\right).19=152\)
\(35:x+3=8\)
\(35:x=5\)
\(x=7\)
8 tháng 8 2023
4) \(\left(x-250\right)\div6=4^3-2^2\times3\)
\(\left(x-250\right)\div6=64-4\times3\)
\(\left(x-250\right)\div6=64-12=52\)
\(x-250=52\times6=312\)
\(x=312+250\)
\(x=562\)
5) \(2x+3x+5x=1030\)
\(x\left(2+3+5\right)=1030\)
\(10x=1030\)
\(x=1030\div10\)
\(x=103\)
6) \(15x-35x+50x=120\)
\(x\left(15-35+50\right)=120\)
\(30x=120\)
\(x=120\div30\)
\(x=4\)
7) \(\dfrac{1}{2}x+\dfrac{1}{6}x+\dfrac{1}{3}x=2023\)
\(x\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{6}\right)=2023\)
\(x\times1=2023\)
\(x=2023\)
8) \(165-\left(35\div x+3\right)\times19=13\)
\(\left(35\div x+3\right)\times19=165-13\)
\(\left(35\div x+3\right)\times19=152\)
\(35\div x+3=152\div19=8\)
\(35\div x=8-3=5\)
\(x=35\div5\)
\(x=7\)
CM
10 tháng 8 2019
Đáp án A
P T ⇔ 2 x 2 2 − 5 2 x + 2 = 0 ⇔ 2 x = 2 2 x = 1 2 ⇔ x = 1 x = − 1 ⇒ S = − 1 ; 1
PT
1
CM
19 tháng 12 2017
Đáp án A.
Đặt t = 2 x , t > 0 ⇒ pt ⇔ 2 t 2 - 5 t + 2 = 0 ⇔ [ t = 2 t = 1 2 ⇔ [ 2 x = 2 2 x = 1 2 ⇔ [ x = 1 x = - 1 ⇒ x 1 + x 2 = 0 .
PT
1
PT
1
CM
26 tháng 1 2017
Đáp án B
Ta có: 2.5 x + 2 + 5.2 x + 2 ≤ 133. 10 x ⇔ 50.5 x + 20.2 x ≤ 133 10 x chia hai vế bất phương trình cho 5 x ta được:
50 + 20.2 x 5 x ≤ 133 10 x 5 x ⇔ 50 + 20. 2 5 x ≤ 133. 2 5 x 1
Đặt t = 2 5 x , t ≥ 0 phương trình (1) trở thành: 20 t 2 − 133 t + 50 ≤ 0 ⇔ 2 5 ≤ t ≤ 25 4
Khi đó ta có: 2 5 ≤ 2 5 x ≤ 25 4 ⇔ 2 5 2 ≤ 2 5 x ≤ 2 5 4 ⇔ − 4 ≤ x ≤ 2 nên a = − 4 , b = 2
Vậy b − 2 a = 10 .
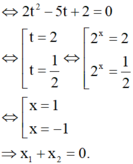
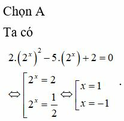
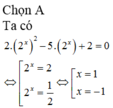
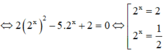
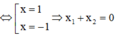
5.2x + 2x+2 = 288
=> 5.2x + 2x.22 = 288
=> 5.2x + 2x.4 = 288
=> 2x.(5 + 4) = 288
=> 2x.9 = 288
=> 2x = 288 : 9
=> 2x = 32 = 25
=> x = 5