Góc xOy và yOz là hai góc kề bù.Biết số đo góc xOy=1/3 số đo góc bẹt.Tính yOz
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
13 tháng 6 2019
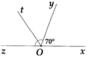
a) Sử dụng tính chất hai góc kề bù,
suy ra y O z ^ = 110°.
Vì Ot là tia phân giác của góc yOz nên y O t ^ = y O z ^ 2 = 55°.
b) Ta có z O t ^ = y O t ^ = 55°. Từ đó, suy ra x O t ^ = 125°.
A
23 tháng 4 2018
x z O y m n
a,Ta có :\(\widehat{xOy}\)và \(\widehat{yOz}\)kề bù ( gt )
\(\Rightarrow\widehat{xOy}+\widehat{yOz}=180^0\)
Mà \(\widehat{xOy}=2\widehat{yOz}\left(gt\right)\)
\(\Rightarrow\widehat{xOy}-180^0:3.2=120^0\)
\(\Rightarrow\widehat{yOz}=180^0-120^0=60^0\)
b,Ta có:
Om là tia phân giác \(\widehat{xOy}\)
\(\Rightarrow\widehat{xOm}=\widehat{mOy}=\frac{\widehat{xOy}}{2}=60^0\)
On là tia phân giác \(\widehat{yOz}\)
\(\Rightarrow\widehat{zOn}=\widehat{nOy}=\frac{\widehat{yOz}}{2}=30^0\)
Tia Oy nằm giữa 2 tia Om và On
\(\Rightarrow\widehat{mOy}+\widehat{yOn}=\widehat{mOn}\)
\(60^0+30^0=\widehat{mOn}\)
\(\Rightarrow\widehat{mOn}=90^0\)
TT
25 tháng 4 2021
a) vì xOy và yOz kề bù
=>xOy+yOz=180\(^0\)
80\(^0\)+yOz=180\(^0\)
yOz=100\(^0\)
b)Vì xOy,yOz kề bù=>oy nằm giữa Ox,Oz
Vì Om là Tia phân giác của xOy=>mOy=80\(^0\):2=40 độ
vì oy nằm giữa ox và oz=> Oz và Ox nằm trên hai nửa mp đối nhau bờ Oy mà Om là tia phân giác của xoy=> Om và oz nằm trên hai nửa mp đối nhau bờ oy hai Oy nằm giữa om và oz
Ta có:
mOy+yOz=moz
40 độ + 100 độ =mOz
=>moz=140 độ
Bạn Học Tốt Nha
31 tháng 7 2021
a) \(\widehat{xOm}=\widehat{mOy}=\dfrac{\widehat{xOy}}{2}=\dfrac{62^0}{2}=31^0\)
\(\widehat{yOn}=\widehat{nOz}=\dfrac{180^0-62^0}{2}=90^0-31^0=59^0\)
b) \(\widehat{mOz}=\widehat{zOy}+\widehat{yOm}\)
\(=180^0-62^0+31^0\)
\(=118^0+31^0=149^0\)
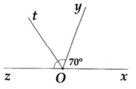
Ta có góc bẹt = 180o
=> Số đo góc xOy là
1/3 x 180o = 60o
Số đo góc yOz là
180o - 60o = 120o
O z x y
Vì \(\widehat{xOy}\)và\(\widehat{yOz}\)là hai góc kề bù.
=> \(\widehat{xOy}+\widehat{yOz}=\widehat{xOz}\)
=> \(\frac{1}{3}\widehat{xOz}+\widehat{yOz}=\widehat{xOy}\)
hay \(\frac{1}{3}\widehat{xOz}+\widehat{yOz}=180^0\)
\(\Rightarrow60^0+\widehat{yOz}=180^0\)
\(\Rightarrow\widehat{yOz}=180^0-60^0=120^0\)