Cho góc nhọn xOy. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB.
Kẻ AC ⊥ Oy; BD ⊥ Ox. Đường thẳng vuông góc với Ox kẻ từ A cắt đường thẳng vuông góc với
Oy kẻ từ B tại M. Chứng minh OM, AC, BD đồng quy.
HELP ME, THANKS .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 6 2023
a: Xét ΔODB vuông tại D và ΔOCA vuông tại C có
OA=OB
góc O chung
=>ΔODB=ΔOCA
=>OD=OC
=>AD=CB
Xét ΔIDA vuông tại D và ΔICB vuông tại C có
DA=CB
góc IAD=góc IBC
=>ΔIDA=ΔICB
=>IA=IB
b: IA=IB
IB>IC
=>IA>IC
2 tháng 1 2022
a) Xét ΔOBC và ΔOAD , có :
góc O chung
OB = OA ( gt )
OC = OD ( gt )
=> ΔOBC = ΔOAD ( c.g.c )
=> AD = BC ( 2 cạnh tương ứng ) ( đpcm )
=> góc OCB = góc ODA ( 2 góc tương ứng )
1 tháng 1 2022
a: Xét ΔOAD và ΔOBC có
OA=OB
\(\widehat{O}\) chung
OD=OC
Do đó: ΔOAD=ΔOBC
Suy ra: AD=BC
5 tháng 1 2022
a: Xét ΔOAD và ΔOBC có
OA=OB
\(\widehat{AOD}\) chung
OD=OC
Do đó: ΔOAD=ΔOBC
Suy ra: AD=BC
S
19 tháng 12 2022
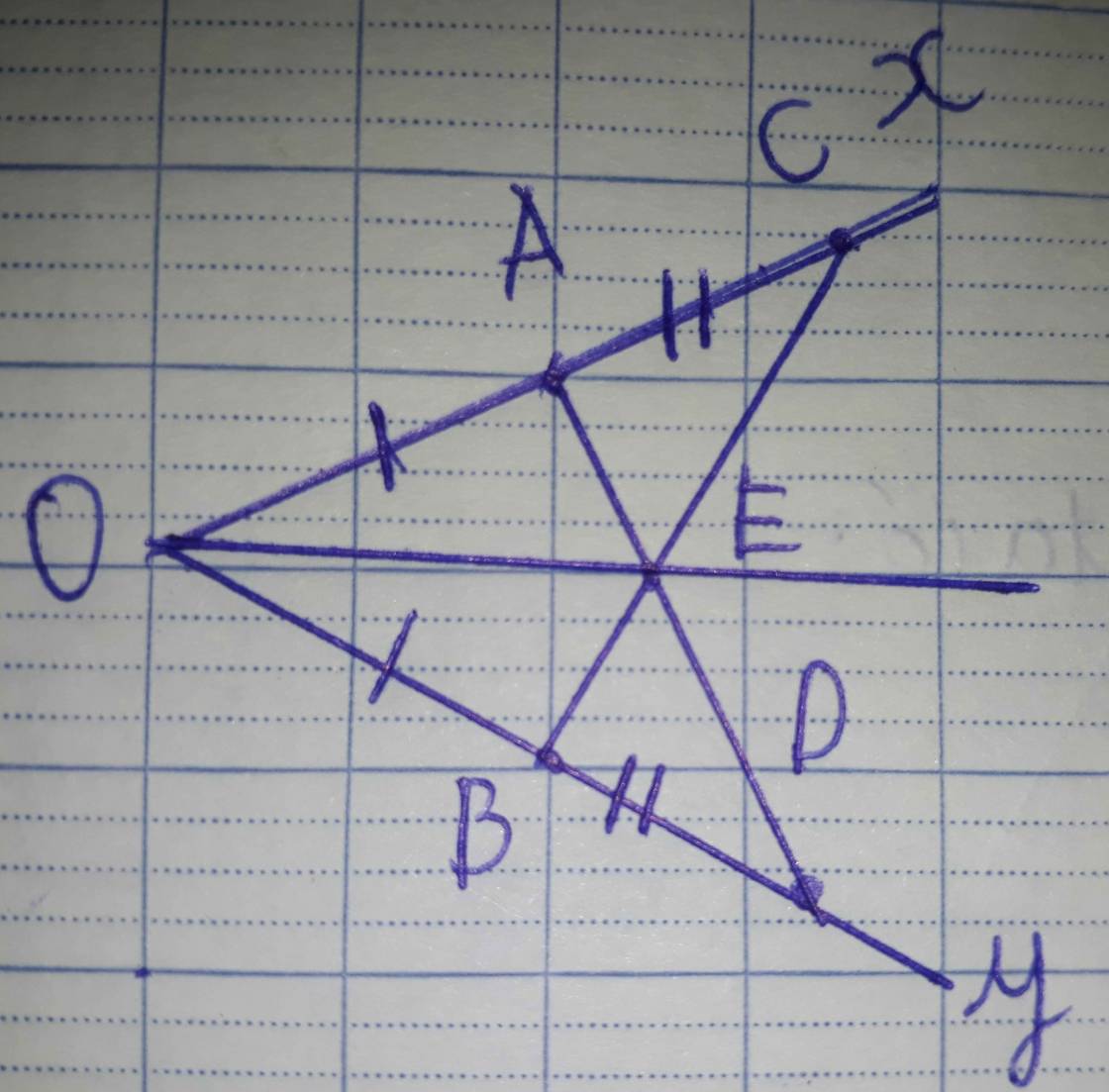
a) xét ΔOCB và ΔODA, ta có :
OA = OB (giả thiết)
\(\widehat{O}\) là góc chung
AC = BD (giả thiết)
⇒ ΔOCB = ΔODA (c.g.c)
⇒ AC = BD (2 cạnh tương ứng)
b) xét ΔEAC và ΔEBD, ta có :
AD = BC (câu a)
\(\widehat{AEC}=\widehat{BED}\) (vì là 2 góc đối đỉnh)
AC = BD (giả thiết)
⇒ ΔEAC = ΔEBD (C.G.C)
c) xét ΔOAE và ΔOBE, ta có :
OA = OB (giả thiết)
AE = BE [vì ΔEAC = ΔEBD (2 cạnh tương ứng)]
OE là cạnh chung
⇒ ΔOAE = ΔOBE (c.c.c)
⇒ \(\widehat{AOE}=\widehat{BOE}\) (2 góc tương ứng)
5 tháng 7 2023
a: Xét ΔAOC vuông tại C và ΔBOD vuông tại D có
OA=OB
góc O chung
=>ΔAOC=ΔBOD
b: góc CAO+góc IAB=góc OAB
góc OBD+góc IBA=góc OBA
mà góc CAO=góc OBD và góc OAB=góc OBA
nên góc IAB=góc IBA
=>ΔIAB cân tại I
c: IC=ID
ID<IA
=>IC<IA
hình bạn tự vẽ nha
có: MA⊥Ox(gt)=>△OAM vuông tại A
MB⊥Oy(gt)=>△OBM vuông tại B
xét △ vuông OAM và △vuông OBM có:
OA=OB(gt)
OM chung
=> △ vuông OAM = △vuông OBM ( cạnh huyền cạnh góc vuông )
=> AM=BM( 2 cạnh tương ứng )
=> M thuộc đường trung trực của AB
mà OA=OB(gt)=> O thuộc đường trung trực của AB
=> OM là đường trung trực của AB hay OM⊥AB
trong △ OAB có:
AC⊥OB=> AC là đường cao thứ nhất của △ OAB
BD⊥OA=> BD là đường cao thứ hai của △ OAB
OM⊥AB=> OM là đường cao thứ ba của △ OAB
=> AC,BD, OM đồng quy tại 1 điểm