cách tính góc tạo bởi đường thẳng y=ax+b với trục Ox
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TL
0
N
1
30 tháng 11 2021
Vì 2>0 nên góc tạo đc là góc nhọn
Ta có hệ số góc của đths là 2
Gọi góc cần tìm là \(\alpha< 90^0\)
\(\Rightarrow\tan\alpha=2\approx\tan63^0\\ \Rightarrow\alpha\approx63^0\)
Vậy góc tạo bởi đths và Oc xấp xỉ 63 độ
HQ
Hà Quang Minh
Giáo viên
12 tháng 9 2023
b)
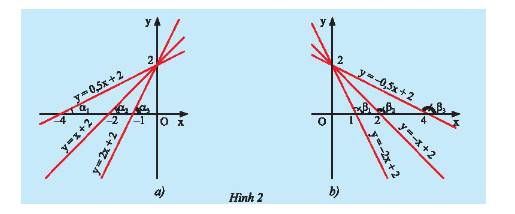
- Ở hình 2a là đồ thị của 3 hàm số \(y = 0,5x + 2;y = x + 2;y = 2x + 2\).
Ta có: \({a_1} = 0,5;{a_2} = 1;{a_3} = 2\) nên \({a_1} < {a_2} < {a_3}\).
Ta có: \({\alpha _1} < {\alpha _2}\) (góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó).
\({\alpha _2} < {\alpha _3}\) (góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó).
Do đó, \({\alpha _1} < {\alpha _2} < {\alpha _3}\).
- Ở hình 2b là đồ thị của 3 hàm số \(y = - 2x + 2;y = - x + 2;y = - 0,5x + 2\).
Ta có: \({a_1} = - 2;{a_2} = - 1;{a_3} = - 0,5\) nên \({a_1} < {a_2} < {a_3}\).
Ta có: \({\beta _1} < {\beta _2}\) (góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó).
\({\beta _2} < {\beta _3}\) (góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó).
Do đó, \({\beta _1} < {\beta _2} < {\beta _3}\).
7 tháng 2 2021
- Gọi phương trình đường thẳng cần tìm có dạng : y = ax + b
- Thay tọa độ của điểm O và P và hàm số ta được hệ :
\(\left\{{}\begin{matrix}0a+b=0\\a\sqrt{3}+b=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=0\\a=\dfrac{\sqrt{3}}{3}\end{matrix}\right.\)
=> Phương trình đường thẳng là : \(y=\dfrac{\sqrt{3}}{3}x\)
\(\Rightarrow Tan\alpha=a=\dfrac{\sqrt{3}}{3}\)
\(\Rightarrow\alpha=30^o\)
Vậy ...
8 tháng 12 2023
a: Vì (d)//y=1/2x+1 nên \(\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b\ne1\end{matrix}\right.\)
Vậy: (d): \(y=\dfrac{1}{2}x+b\)
Thay x=2 và y=2 vào (d), ta được:
\(b+\dfrac{1}{2}\cdot2=2\)
=>b+1=2
=>b=1
vậy: (d): \(y=\dfrac{1}{2}x+1\)
b: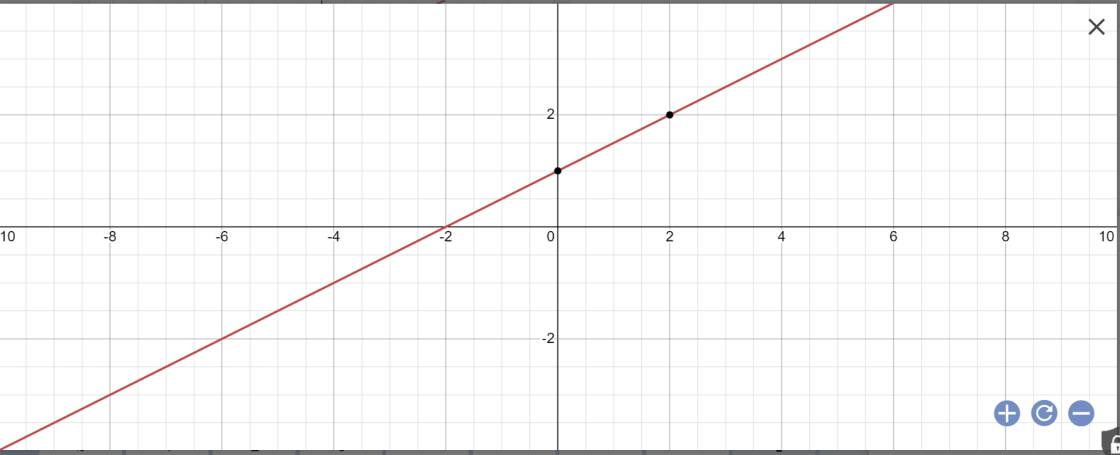 
c: Gọi \(\alpha\) là góc tạo bởi (d) với trục Ox
Ta có: (d): \(y=\dfrac{1}{2}x+1\)
=>a=1/2
=>\(tan\alpha=a=\dfrac{1}{2}\)
=>\(\alpha\simeq26^034'\)
d: tọa độ B là:
\(\left\{{}\begin{matrix}y=0\\\dfrac{1}{2}x+1=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\\dfrac{1}{2}x=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=-2\end{matrix}\right.\)
Tọa độ C là;
\(\left\{{}\begin{matrix}x=0\\y=\dfrac{1}{2}x+1=\dfrac{1}{2}\cdot0+1=1\end{matrix}\right.\)
Vậy: B(-2;0); C(1;0)
\(OB=\sqrt{\left(-2-0\right)^2+\left(0-0\right)^2}=\sqrt{2^2+0^2}=2\)
\(OC=\sqrt{\left(1-0\right)^2+\left(0-0\right)^2}=\sqrt{1^2+0^2}=1\)
Vì Ox\(\perp\)Oy nên OB\(\perp\)OC
=>ΔBOC vuông tại O
=>\(S_{BOC}=\dfrac{1}{2}\cdot OB\cdot OC=\dfrac{1}{2}\cdot2\cdot1=1\)
12 tháng 1 2022
a: Thay x=1 và y=-2 vào y=ax+1, ta được:
a+1=-2
hay a=-3
Vậy: (d'): y=-3x+1
c: Tọa độ giao điểm của (d) và (d') là:
\(\left\{{}\begin{matrix}-3x+1=x+3\\y=x+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\y=3-\dfrac{1}{2}=\dfrac{5}{2}\end{matrix}\right.\)