Lấy bốn điểm A;B;C;D trong đó không có ba diem nao thang hang Ke cac đường thẳng đi qua các cặp điểm.Có tất cả bao nhiêu đường thẳng Đó là những đườg thẳng nào
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


y'yBDACMFE
a) b) Đưa các đẳng thức về dạng đẳng thức của các tỉ số và áp dụng để chứng minh các cặp tam giác đồng dạng.
c) Từ hai phần a và b, ta suy ra \widehat{CAM}=\widehat{MFE}CAM=MFE
a) b) Đưa các đẳng thức về dạng đẳng thức của các tỉ số và áp dụng để chứng minh các cặp tam giác đồng dạng.
c) Từ hai phần a và b, ta suy ra \widehat{CAM}=\widehat{MFE}CAM=MFE.

bài 1:Qua điểm A và mỗi điểm B,C,D có ba đường thằng là AB, AC,AD. Qua điểm B và mỗi điểm C,D có hai đường thẳng là BC,BD (Không qua A). Qua điểm C và D còn lại có một đường thẳng CD (không đi qua A,B).
Chú ý: có thể trình bày ngắn gọn như sau : với 4 điểm A,B,C,D thì có 6 đường thẳng AB,AC,AD,BC,BD,CD
bài 2:Vì 3 điểm M,N,P thẳng hàng nên đường thẳng đi qua cả 3 điểm M,N,P trùng nhau và Q nằm ngoài đường thẳng trên nên kẻ được 3 đường thẳng lần lượt đi qua 3 điểm thẳng hàng.
Vậy ta có 4 đường thẳng: MP,QN,QM,QP(không kể MN, NP)

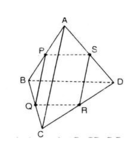
a) Ta có:
PQ = (ABC) ∩ (PQRS)
RS = (PQRS) ∩ (ACD)
AC = (ABC) ∩ (ACD)
Vậy hoặc PQ, RS, AC đồng qui hoặc song song.
b) PS =(ABD) ∩ (PQRS)
RQ = (BCD) ∩ (PQRS)
BD = (ABD) ∩ (CBD)
Vậy PS, RQ, BD đồng quy hoặc song song.

(Tự vẽ hình)
Không mất tính tổng quát giả sử điểm A nằm giữa hai điểm O, B và điểm D nằm giữa hai điểm O,C.
Theo bài ra ta có: \(OA.OB=OC.OD\Leftrightarrow\frac{OA}{OC}=\frac{OD}{OB}\)
Kết hợp với \(\widehat{AOD}=\widehat{COB}\) (hai góc trùng nhau), ta được \(\Delta OAD\) \(\sim\)\(\Delta OCB\) (c.g.c).
Suy ra \(\widehat{ADO}=\widehat{CBO}\), do đó ABCD là tứ giác nội tiếp.
Vậy A, B, C, D cùng thuộc một đường tròn