mn giúp mink bài 4 tìm Y với, mình cần gấp.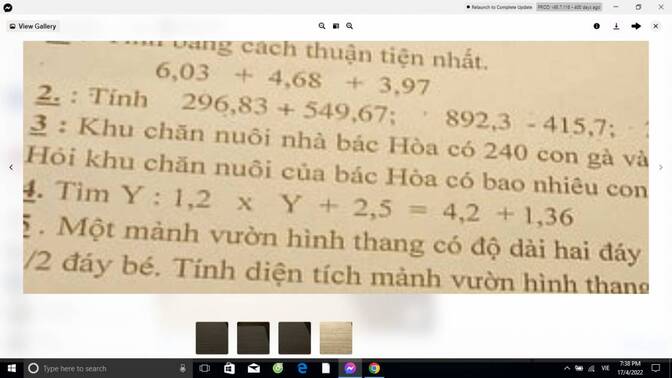
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bài 4:
a: Ta có: \(-\left|x+1.1\right|\le0\forall x\)
\(\Leftrightarrow-\left|x+1.1\right|+1.5\le1.5\forall x\)
Dấu '=' xảy ra khi x=-1,1
b: Ta có: \(-4\left|x-2\right|\le0\forall x\)
\(\Leftrightarrow-4\left|x-2\right|+10\le10\forall x\)
Dấu '=' xảy ra khi x=2
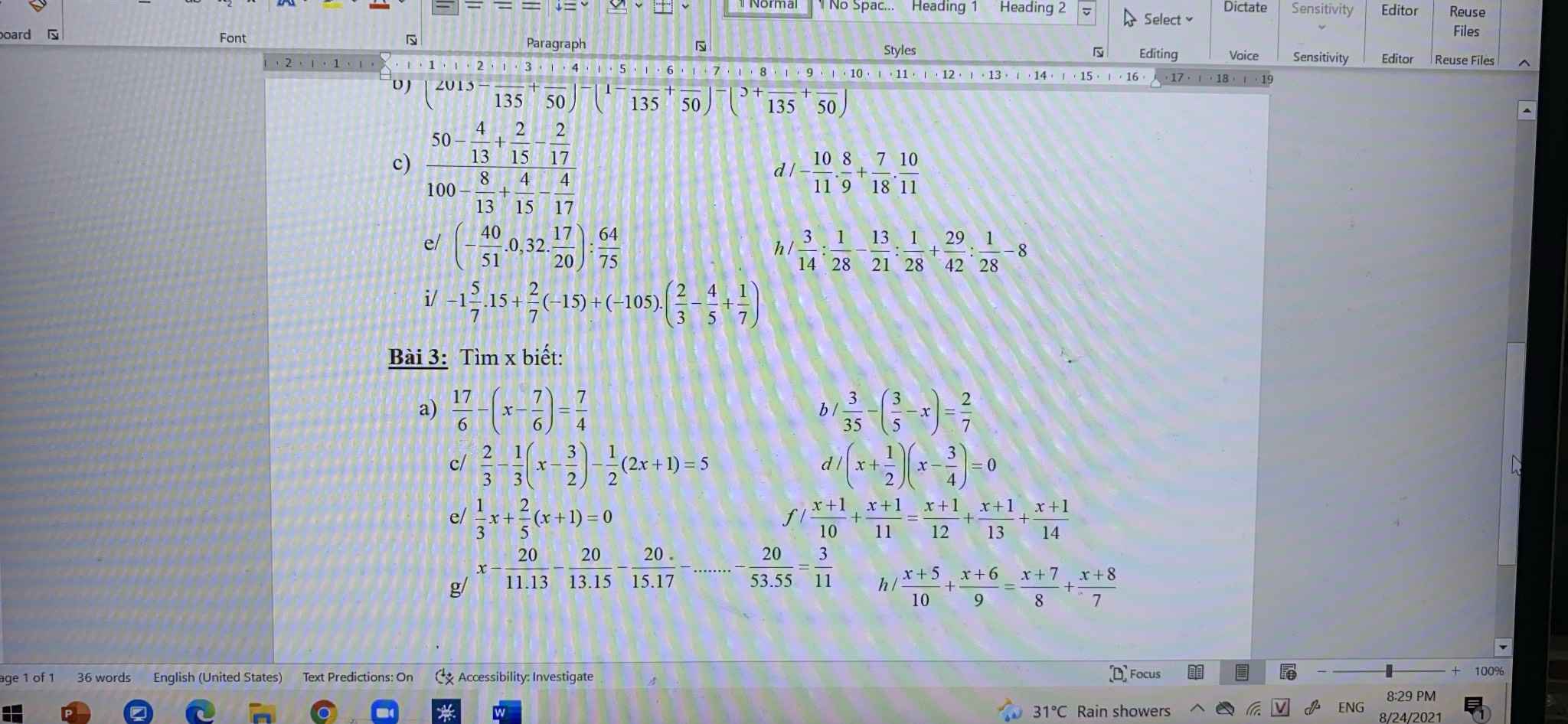
các bạn ơi giúp mink bài 3 với nha mink cần gấp tối nay rồi ! ![]()
giúp mink với nha mink cảm ơn nhìu lắm



Gọi số tự nhiên đó là \(n\).
Số tự nhiên đó khi chia cho \(3,4,5,10\)có số dư lần lượt là \(2,3,4,9\)nên \(n+1\)chia hết cho cả \(3,4,5,10\)
mà \(n\)nhỏ nhất nên \(n+1=BCNN\left(3,4,5,10\right)\).
Phân tích thành tích các thừa số nguyên tố: \(3=3,4=2^2,5=5,10=2.5\)
suy ra \(BCNN\left(3,4,5,10\right)=2^2.3.5=60\)
suy ra \(n+1=60\Leftrightarrow n=59\).
Tìm x, y, z thoả mãn đẳng thức
x+y+z +8=2√(x-1) +4√(y-2) +6√(z-3)
Mn giúp mình với , mình cần gấp lắm

\(x+y+z+8=2\sqrt{x-1}+4\sqrt{y-2}+6\sqrt{z-3}\) (ĐKXĐ : \(x\ge1;y\ge2;z\ge3\))
\(\Leftrightarrow\left(x-1-2\sqrt{x-1}+1\right)+\left(y-2-4\sqrt{y-2}+4\right)+\left(z-3-6\sqrt{z-3}+9\right)=0\)
\(\Leftrightarrow\left(\sqrt{x-1}-1\right)^2+\left(\sqrt{y-2}-2\right)^2+\left(\sqrt{z-3}-3\right)^2=0\)
Vì \(\left(\sqrt{x-1}-1\right)^2\ge0;\left(\sqrt{y-2}-2\right)^2\ge0;\left(\sqrt{z-3}-3\right)^2\ge0\)
nên phương trình tương đương với : \(\hept{\begin{cases}\left(\sqrt{x-1}-1\right)^2=0\\\left(\sqrt{y-2}-2\right)^2=0\\\left(\sqrt{z-3}-3\right)^2=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=2\\y=6\\z=12\end{cases}}}\)(TMĐK)
Vậy nghiệm của phương trình : \(\left(x;y;z\right)=\left(2;6;12\right)\)

Bài 2:
a: Xét ΔABC có
BI,CI là các đường phân giác
BI cắt CI tại I
Do đó: I là tâm đường tròn nội tiếp ΔABC
b: Ta có: \(\widehat{DIB}=\widehat{IBC}\)(hai góc so le trong, DI//BC)
\(\widehat{DBI}=\widehat{IBC}\)(BI là phân giác của góc DBC)
Do đó: \(\widehat{DIB}=\widehat{DBI}\)
=>ΔDIB cân tại D
c: Ta có: \(\widehat{EIC}=\widehat{ICB}\)(hai góc so le trong, EI//BC)
\(\widehat{ECI}=\widehat{ICB}\)(CI là phân giác của góc ECB)
Do đó: \(\widehat{EIC}=\widehat{ECI}\)
=>ΔEIC cân tại E
d: Ta có: ΔDIB cân tại D
=>DB=DI
Ta có: ΔEIC cân tại E
=>EI=EC
Ta có: DI+IE=DE
mà DI=DB
và EC=EI
nên DB+EC=DE
Bài 1:
a: Xét ΔABC có
BE,CF là các đường phân giác
BE cắt CF tại I
Do đó: I là tâm đường tròn nội tiếp ΔABC
=>AI là phân giác của góc BAC
b: ta có: \(\widehat{ABE}=\widehat{CBE}=\dfrac{\widehat{ABC}}{2}\)(BE là phân giác của góc ABC)
\(\widehat{ACF}=\widehat{FCB}=\dfrac{\widehat{ACB}}{2}\)(CF là phân giác của góc ACB)
mà \(\widehat{ABC}=\widehat{ACB}\)
nên \(\widehat{ABE}=\widehat{EBC}=\widehat{ACF}=\widehat{FCB}\)
c: ta có: \(\widehat{EBC}=\widehat{FCB}\)
=>\(\widehat{IBC}=\widehat{ICB}\)
=>ΔIBC cân tại I
d: Xét ΔABE và ΔACF có
\(\widehat{ABE}=\widehat{ACF}\)
AB=AC
\(\widehat{BAE}\) chung
Do đó: ΔABE=ΔACF
=>BE=CF
e:
Ta có: ΔAEB=ΔAFC
=>AE=AF
Ta có: AE+EC+AC
AF+FB=AB
mà AE=AF
và AC=AB
nên EC=FB
Xét ΔFIB và ΔEIC có
FB=EC
\(\widehat{FBI}=\widehat{ECI}\)
BI=CI
Do đó: ΔFIB=ΔEIC
 mn giúp mink với. mình cần gấp trong tối nay.
mn giúp mink với. mình cần gấp trong tối nay.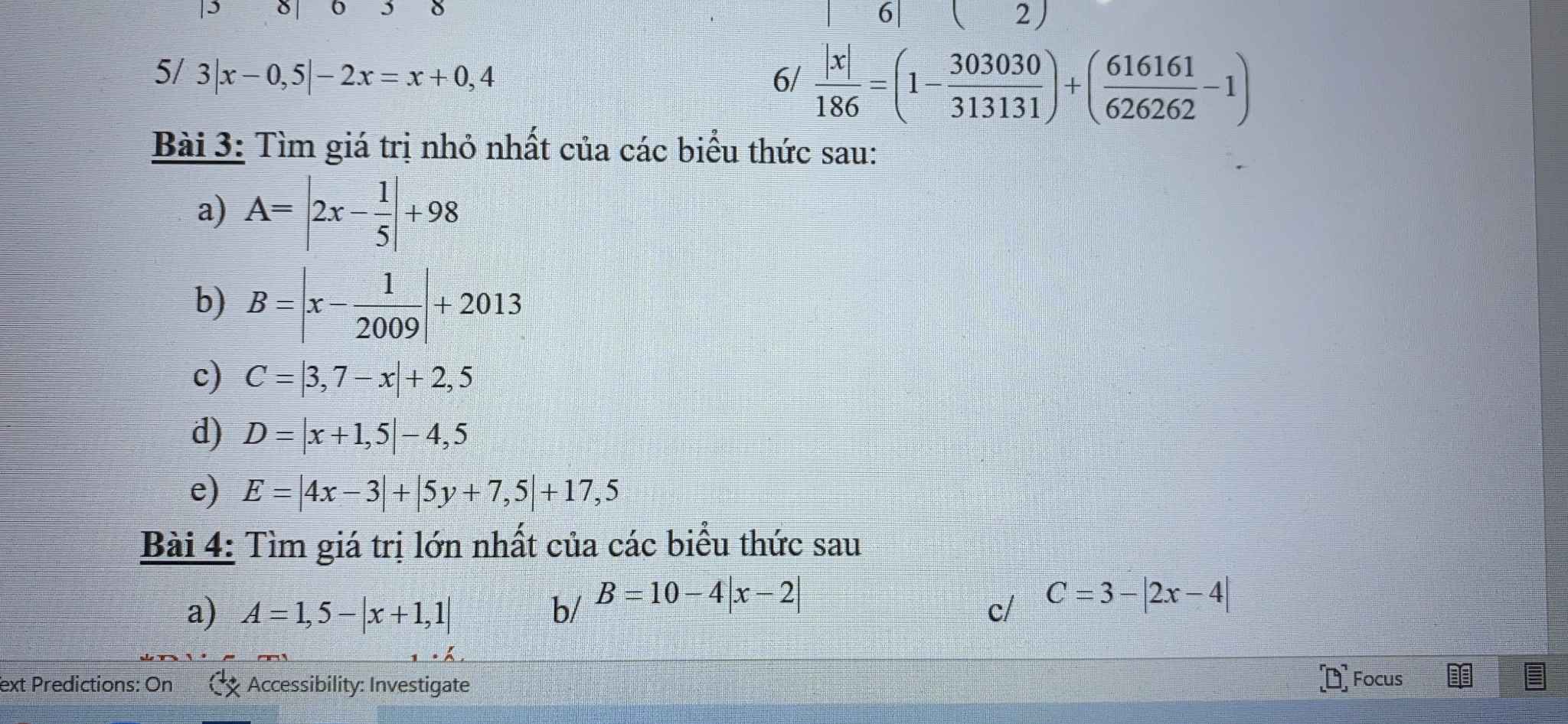


1,2 x Y + 2,5 = 4,2 + 1,36
1,2 x Y + 2,5 = 5,56
1,2 x Y = 5,56 - 2,5
1,2 x Y = 3,06
Y = 3,06 : 1,2
Y = 2,55
vậy Y = ...
1,2 x Y + 2,5 = 4,2 + 1,36
1,2 x Y + 2,5 = 5,56
1,2 x Y = 5,56 - 2,5
1,2 x Y = 3,06
Y = 3,06 : 1,2
Y = 2,55
mình viết bừa :) tích cho mình nha