Giúp mình câu 17 và 43 vs ạ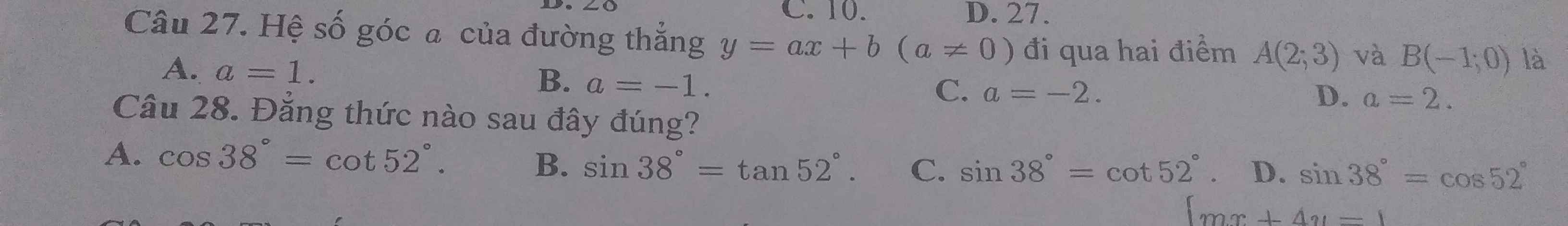
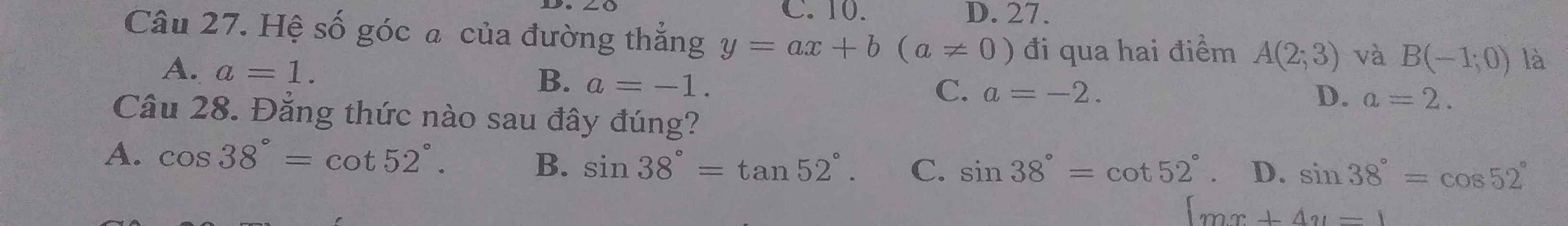
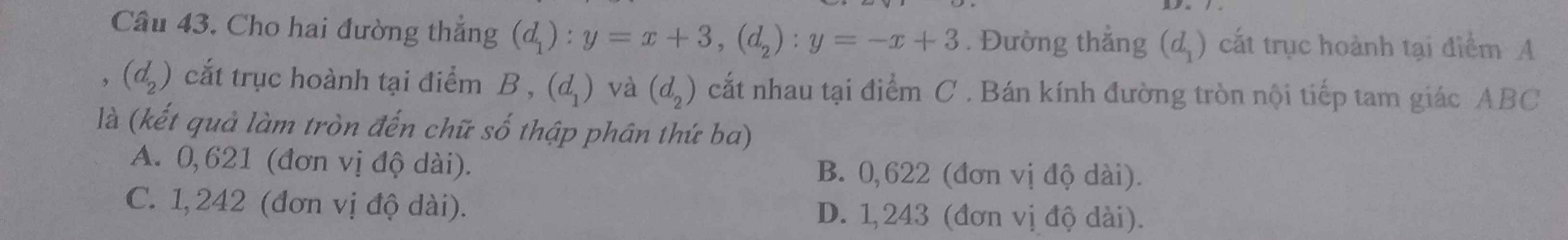
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan



NT
0



NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 9 2021
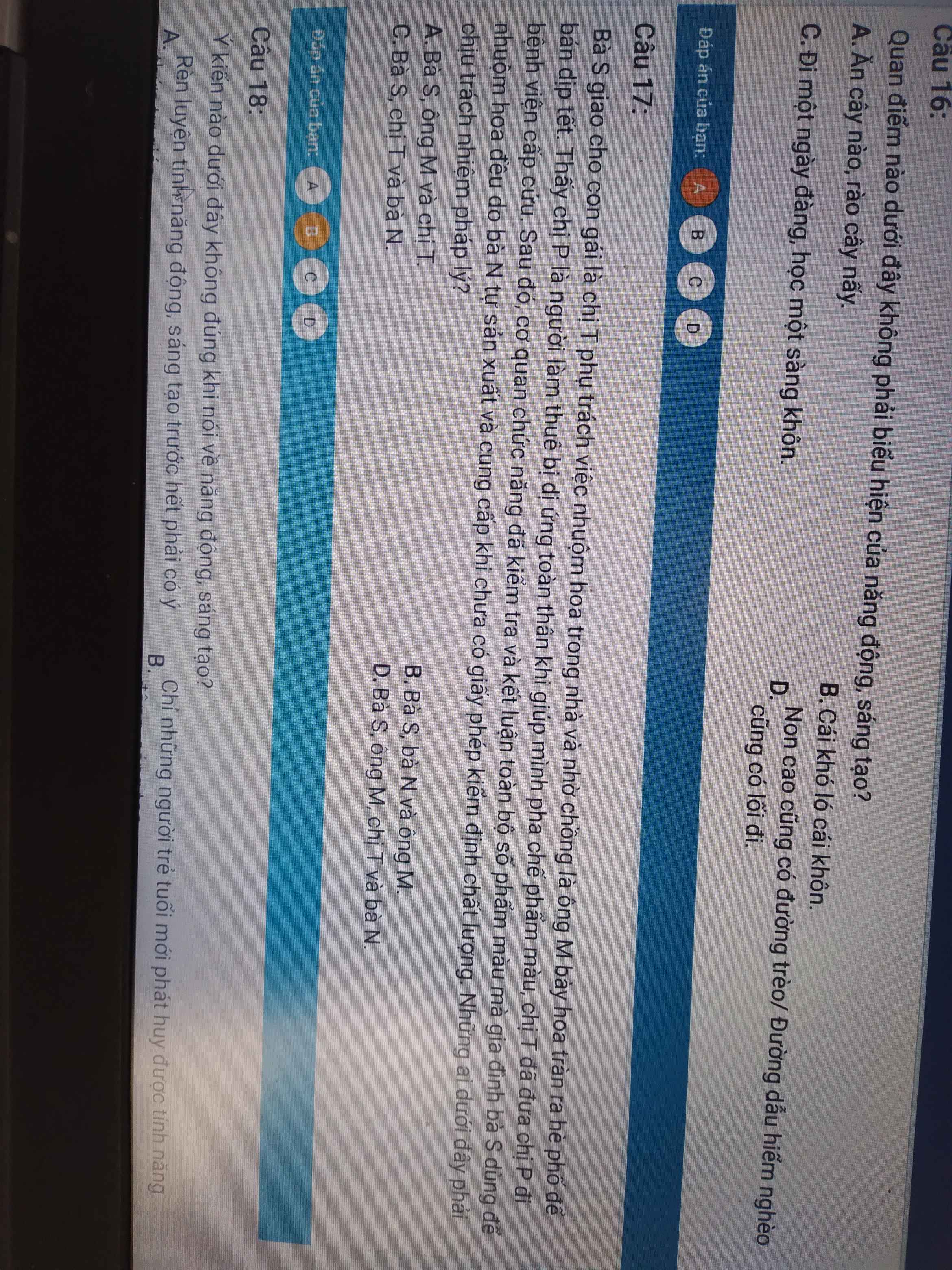
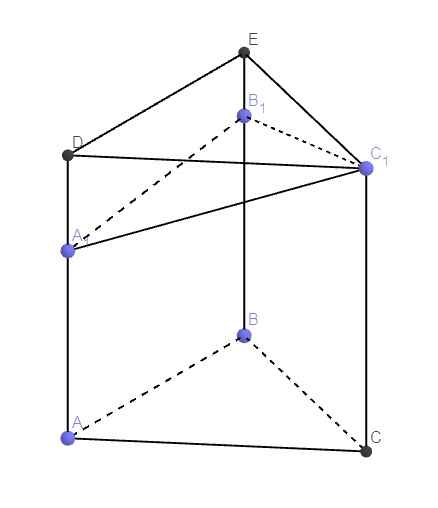
17.
Câu 17 này đề bài sai (ở độ dài AB, nếu ko nhìn lầm thì AB=41 là 1 con số phi lý)
Cách tính như sau:
Qua \(C_1\) kẻ các đường thẳng song song AC và BC, cắt \(AA_1\) và \(BB_1\) kéo dài tại D và E
\(\Rightarrow ABC.DEC_1\) là lăng trụ đứng có thể tích V
\(V=CC_1.S_{ABC}=6.\dfrac{AB^2\sqrt{3}}{4}=\dfrac{3AB^2\sqrt{3}}{2}\)
Gọi thể tích khối đa diện cần tính là \(V_1\)
\(\Rightarrow\dfrac{V_1}{V}=\dfrac{1}{3}\left(\dfrac{AA_1}{AD}+\dfrac{BB_1}{BE}+\dfrac{CC_1}{CC_1}\right)=\dfrac{5}{6}\)
\(\Rightarrow V_1=\dfrac{5}{6}V=...\)

13 tháng 12 2021
17[21-(-111)]+17[29-121]=17.132+17.(-92)=17.[132+(-92)]=17.40=680






28D
27: Theo đề, ta có hệ:
\(\left\{{}\begin{matrix}a\cdot2+b=3\\a\cdot\left(-1\right)+b=0\end{matrix}\right.\Leftrightarrow a=1\)
=>Chọn A
43:
tọa độ A là;
y=0 và x+3=0
=>A(-3;0)
Tọa độ B là;
-x+3=0 và y=0
=>B(3;0)
Tọa độ C là;
x+3=-x+3 và y=x+3
=>x=0 và y=3
=>C(0;3)
A(-3;0); B(3;0); C(0;3)
\(AB=\sqrt{\left(3+3\right)^2+\left(0-0\right)^2}=6\)
\(AC=\sqrt{\left(0+3\right)^2+\left(3-0\right)^2}=3\sqrt{2}\)
BC=căn (0-3)^2+(3-0)^2=3*căn 2(cm)
Vì BC^2+AC^2=AB^2 và BC=AC
nên ΔABC vuông cân tại B
P=1/2(3căn 2+3căn 2+6)=3căn 2+3(cm)
S=1/2*3*căn 2*3*căn 2=9
=>r=9/3căn 2+3=-3+3căn 2=1,243
=>Chọn D