Chứng minh x=-1 là nghiệm của đa thức 3x4+x3+10x2-7.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Thay x = 0 vào đa thức 5x + 10x2, ta có:
5.0 + 10.02 = 0 + 0 = 0
Thay x= - 1/2 vào đa thức 5x + 10x2, ta có:
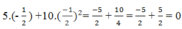
Suy ra x = 0; x= (-1)/2 là các nghiệm của đa thức 5x + 10x2.

Thay x = 0 vào đa thức 5x + 10x2, ta có:
5.0 + 10.02 = 0 + 0 = 0
Thay x= - 1/2 vào đa thức 5x + 10x2, ta có:
Suy ra x = 0; x= (-1)/2 là các nghiệm của đa thức 5x + 10x2.
Thay x = 0 vào đa thức 5x + 10x2, ta có:
5.0 + 10.02 = 0 + 0 = 0
Thay x= - 1/2 vào đa thức 5x + 10x2, ta có:
Suy ra x = 0; x= (-1)/2 là các nghiệm của đa thức 5x + 10x2.

P(x)=3x^4+2x^2+2
Ta có 3x^4 >=0 , 2x^2 >=0 =. P(x)>0
Vậy P(x) vô nghiêm
Học tốt
Ta có: P(x) = 4x3 + 3x4 - 2x2 - x3 + 4x2 - 3x3 + 2
P(x) = (4x3 - x3 - 3x3) + 3x4 - (2x2 - 4x2) + 2
P(x) = 3x4 + 2x2 + 2 \(\ge\)2 > 0
(vì 3x4 \(\ge\)0; 2x2 \(\ge\)0; 2 > 0)
=> Đa thức P(x) ko có nghiệm

Cho A(x) = 0, có:
x2 - 4x = 0
=> x (x - 4) = 0
=> x = 0 hay x - 4 = 0
=> x = 0 hay x = 4
Vậy: x = 0; x = 4 là nghiệm của đa thức A(x)

a) \(P\left(x\right)=3x^3-x^2-2x^4+3+2x^3+x+3x^4-x^2-2x^4+3+2x^3+x+3x^4\)
\(=2x^4+7x^3-2x^2+2x+6\)
\(Q\left(x\right)=-x^4+x^2-4x^3-2+2x^2-x-x^3-x^4+x^2-4x^3-2+2x^2-x-x^3\)
\(=-2x^4-10x^3+6x^2-2x-4\)
b) \(P\left(x\right)+Q\left(x\right)=2x^4+7x^3-2x^2+2x+6-2x^4-10x^3+6x^2-2x-4\)
\(=-3x^3+4x^2+2\)

a)⇔A= x4+2x3-5x+9+2x4-2x3= 3x4-5x+9
⇔B= 2x2-6x+2-3x4-2x2+3x-4= -3x4-3x-2
b)A(x)+B(x)= 3x4-5x+9-3x4-3x-2= -8x+7
A(x)-B(x)= 3x4-5x+9+3x4+3x+2= 6x4-2x+1
c)C(x) có hệ số tự do bằng 0 nên có nghiệm bằng 0
d)A(x)+5x= 3x4+9. Tại x bất kì thì 3x4≥0 ⇔ 3x4+9 ≥ 9 ≥ 0
⇒ H(x) vô nghiệm
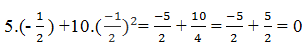
F(-1)=3*(-1)^4+(-1)^3+10*(-1)^2-7
=3-1+10-7
=5
=>x=-1 ko là nghiệm của 3x^4+x^3+10x^2-7