Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB=AA'=a, AC'=2a. Tìm đường vuông góc chung giữa AC' và CD', tính khoảng cách giữa chúng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

28 tháng 6 2023
C đáy=36:3=12cm
=>BC=12:2-4=2cm
S đáy=2*4=8cm2
V=8*3=24cm3

HN
5 tháng 4 2022
AC'=\(\sqrt{AB^2+AD^2+AA'^2}\)=\(\sqrt{3^2+4^2+5^2}\)=5\(\sqrt{2}\).

HN
5 tháng 4 2022
AC'=\(\sqrt{AB^2+AD^2+AA'^2}\)=\(\sqrt{3^2+4^2+5^2}\)=5\(\sqrt{2}\).


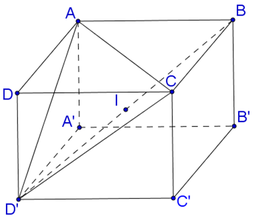

ABB'A' và CDD'C' là hình vuông \(\Rightarrow CD'\perp DC'\Rightarrow CD'\perp\left(ADC'B'\right)\)
Gọi M là giao điểm CD' và DC' \(\Rightarrow\) M là trung điểm 2 đoạn nói trên
Trong mp (ADC'B'), từ M kẻ \(MH\perp AC'\Rightarrow MH\) là đường vuông góc chung của AC' và CD'
\(DC'=AB'=\sqrt{AB^2+A'A^2}=a\sqrt{2}\)
\(\Rightarrow AD=B'C'=\sqrt{AC'^2-AB'^2}=a\sqrt{2}\)
\(\Rightarrow\Delta ADC'\) vuông cân tại D \(\Rightarrow\Delta MHC'\) vuông cân tại H
\(\Rightarrow MH=\dfrac{MC'}{\sqrt{2}}=\dfrac{DC'}{2\sqrt{2}}=\dfrac{a}{2}\)