vẽ hai dường thẳng xx' và yy' tại I sao cho góc xIy bằng 35 dộ tính số do các góc còn lại
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


x x' y y' O 45 độ
ta có: xx' cắt yy' tại O
=> góc xOy = góc x'Oy' =45 độ ( đối đỉnh)
=> góc x'Oy' = 45 độ
mà góc xOy + góc x'Oy = 180 độ ( kề bù)
Thay số: 45 độ + góc x'Oy = 180 độ
góc x'Oy = 180 độ - 45 độ
góc x'Oy = 135 độ
mà góc x'Oy = góc xOy' = 135 độ ( đối đỉnh)
=> góc xOy' = 135 độ

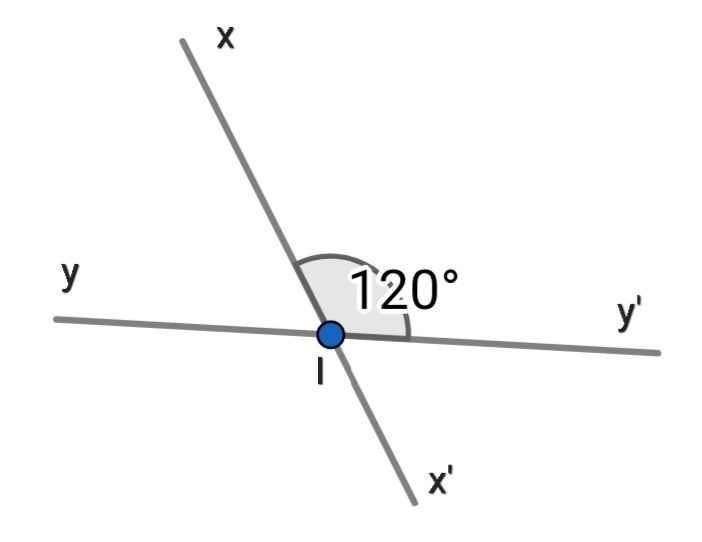 Do ∠x'Iy và ∠xIy' là hai góc đối đỉnh
Do ∠x'Iy và ∠xIy' là hai góc đối đỉnh
⇒ ∠x'Iy = ∠xIy' = 120⁰

O x x' y y' 30 độ
Ta có : x'Oy' = xOy (vì là 2 góc đối đỉnh)
Mà xOy = 30o (đề bài)
=> x'Oy' = 30o
Ta có : xOy + yOx' = 180o (vì là 2 góc kề bù)
Mà xOy = 30o
=> 30o + yOx' = 180o
=> yOx' = 180o - 30o
=> yOx' = 150o
Ta có : x'Oy = y'Ox (vì là 2 góc đối đỉnh)
Mà x'Oy = 150o (đề bài)
=> y'Ox = 150o

O y x' x y' 47 0
Giả sử hai đường thẳng \(xx'\)và \(yy'\)cắt nhau tại O và \(\widehat{xOy}=47^0\)
\(\Rightarrow\widehat{x'Oy'}=\widehat{xOy}=47^0\)đối đỉnh
\(\widehat{xOy'}=180^0-\widehat{xOy}=180^0-47^0=133^0\)
do \(\widehat{xOy}\)và \(\widehat{xOy'}\)kề bù và \(\widehat{x'Oy}=\widehat{xOy'}=133^0\)
Bài 2 : Ta có hình vẽ :
y O y' x x' z' z Hình hơi lệch tí nên thông cảm nhé
Các cặp góc bằng nhau là : \(\widehat{xOy}=\widehat{x'Oy'};\widehat{yOz}=\widehat{y'Oz'}\)

x x' y y' O
Nhận thầy từ hình vẽ hai góc xOy và x'Oy' là hai góc đối đỉnh
Mà xOy = 90 độ => xOy = x'Oy' = 90 độ
Có hai góc xOy + xOy' = 180 độ (kề bù do đối đỉnh)
=> 90 độ + xOy' = 180 độ
=> xOy' = 90 độ
Thấy xOy' và x'Oy đối đỉnh mà xOy' = 90 độ
=> xOy' = x'Oy = 90 độ
a)
x O y x' y' 90*
b)
- góc xOy=x'Oy'=90*(đối đỉnh)
- Vì góc xOy kề bù với yOx'
nên: xOy+yOx'=180*
hay:90*+yOx'=180*
=> yOx'=180*-90*
Vậy yOx'=90*
- yOx'=xOy'=90*(đối đỉnh)
![]() ^...^
^...^ ![]() ^_^
^_^

A1 = 50 o
=> A3 = A1 =50 o ( 2 góc đối đỉnh)
Ta có: A1 + A2 = 180o ( 2 góc kề bù)
=> A2 = 180 o - A1 = 180o - 50o = 130o
=> A4 = A2 = 130o ( 2 góc đối đỉnh)

180-35=\(^{145^0}\)