Một vật sáng AB cao 2cm đặt vuông góc với trục chính của 1 TKHT có tiêu cự 30cm. VẬt AB cách thấu kính 50 cm. Biết điểm A của vật nằm trên trục chính của thấu kính
a/ Dựng ảnh
b/Ảnh thật hay ảnh ảo?Tại sao ?
c/Để ảnh thật cao gấp đôi vật thì phải di chuyển vật đến vị trí cách thấu kính bao nhiêu cm ?
Giúp em với, em đang cần gấp ạ

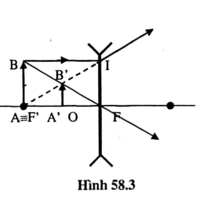
b)Ảnh thật.
c)Để ảnh thật cao gấp đôi vật \(\Rightarrow h'=2h\) thì:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{h}{2h}=\dfrac{d}{d'}=\dfrac{1}{2}\Rightarrow d'=2d\)
Khi đó vị trí cách thấu kính là:
\(d'=2d=2\cdot50=100cm\)