Cho a1+a2+...+a1999=1. CMR: a12+a22+...+a19992\(\ge\frac{1}{1999}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: x + y = ( a 1 2 + b 1 ) + ( a 2 2 + b 2 ) = ( a 1 + a 2 ) 2 + ( b 1 + b 2 )
Vì a 1 , a 2 , b 1 , b 2 là các số hữu tỉ nên a 1 + a 2 , b 1 + b 2 cũng là số hữu tỉ.
Lại có: xy = ( a 1 2 + b 1 )( a 2 2 + b 2 ) = 2 a 1 a 2 + a 1 b 2 2 + a 2 b 1 2 + b 1 b 2
= ( a 1 b 2 + a 2 b 1 ) 2 + (2 a 1 a 2 + b 1 b 2 )
Vì a 1 , a 2 , b 1 , b 2 là các số hữu tỉ nên a 1 b 2 + a 2 b 1 , a 1 a 2 + b 1 b 2 cũng là các số hữu tỉ.

Ta có a1 +a2+...+a20 <0
Lại có a2+a3+a4 >0;
a5 +a6+a7 >0;
a8+a9+a10>0;
a11+a12+a13>0;
a15+a16+a17>0;
a18 +a19+a20>0;
a1>0
=> a14<0;
Lại có a1+a2+a3 >0;
a4+a5+a6>0;
....
a10+a11+a12>0;
a15+a16+a17>0;
a18+a19+a20>0;
=> a13+a14<0;
mà a12+a13+a14>0;
=>a12>0;
=> a1.a12>0;
a1.a14+a14.a12<0;
=>a1.a14+a14.a12<a1.a12

Câu hỏi của Vu Kim Ngan - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo nhé!

ta có
a1+(a2+a3+a4)+... +(a11+a12+a13)+a14+(a15+a16+a17)+(a18+a19+a20)<0
a1>0; a2+a3+a4>0;...;a11+a12+a13>0;a15+a16+a17>0;a18+a19+a20>0; a14<0
Ta có:
(a1+a2+a3)+...+(a10+a11+a12)+(a13+a14)+(a15+a16+a17)+(a18+a19+a20)<0
=>(a13+a14)<0
có a12+a13+a14>0=>a12>0
Từ các cmt suy ra a1>0; a12>0; a14<0
=>a1. a14+a12.a12<a1.a12(đpcm)

Đáp án A
Chọn x = - 1 ⇒ 1 + 2 12 = a 0 - a 1 + a 2 - a 3 + . . . + a 12 ⇒ S = 3 12
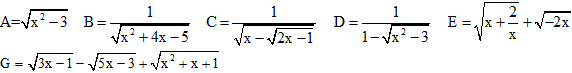 Mn giúp em với ;-;
Mn giúp em với ;-;
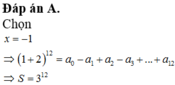
Ta có
a21 + \(\frac{1}{1999^2}\)\(\ge\frac{2a_1}{1999}\)
.............
a21999 + \(\frac{1}{1999^2}\ge2\frac{a_{1999}}{1999}\)
Cộng vế theo vế ta được
a21 + a22 + ...+ a21999 + \(\frac{1}{1999}\)\(\ge\)(a1 + a2 + ...+ a1999 ) \(\frac{2}{1999}\)= \(\frac{2}{1999}\)
<=> a21 + a22 + ...+ a21999 \(\ge\frac{1}{1999}\)