giúp mik làm câu c với
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
20 tháng 12 2021
c: Xét tứ giác ABCK có
M là trung điểm của BK
M là trung điểm của AC
Do đó: ABCK là hình bình hành
Suy ra: AK//BC
20 tháng 12 2021
c: Xét tứ giác ABCK có
M là trung điểm của BK
M là trung điểm của AC
ABCK là hình bình hành
Suy ra: Ak song song BC
kí hiệu AK//BC
NK
3
NN
1
12 tháng 10 2021
a, Áp dụng t/c dtsbn:
\(\dfrac{a}{b}=\dfrac{c}{d}=\dfrac{a+c}{b+d}\)
b, Áp dụng t/c dtsbn:
\(\dfrac{a}{b}=\dfrac{c}{d}=\dfrac{2021a}{2021b}=\dfrac{2021a-c}{2021b-d}\)
c, Ta có \(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\left(\dfrac{a}{b}\right)^2=\left(\dfrac{c}{d}\right)^2\)
Áp dụng t/c dtsbn:
\(\left(\dfrac{a}{b}\right)^2=\left(\dfrac{c}{d}\right)^2=\dfrac{a^2}{b^2}=\dfrac{c^2}{d^2}=\dfrac{a^2+c^2}{b^2+d^2}\)
TD
3
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 2 2022
Theo như hình vẽ thì I là tâm đường tròn ngoại tiếp ABC và J là giao điểm MI với AO đúng không nhỉ?
Tam giác AMJ vuông tại J nên theo Pitago: \(MJ^2=MA^2-AJ^2\)
Tương tự tam giác vuông MJO: \(MJ^2=MO^2-JO^2\)
Trừ vế theo vế: \(MA^2-AJ^2-MO^2+JO^2=0\) (1)
Tam giác vuông AIJ: \(IJ^2=AI^2-AJ^2\)
Tam giác vuông \(IJO\): \(IJ^2=OI^2-JO^2\)
\(\Rightarrow AI^2-AJ^2-OI^2+JO^2=0\) (2)
Trừ vế (1) và (2): \(MA^2-AI^2-MO^2+OI^2=0\) (3)
Do O là trung điểm BC nên \(IO\perp BC\)
\(\Rightarrow OI^2+OC^2=IC^2\)
Do M, C cùng thuộc đường tròn tâm O đường kính BC \(\Rightarrow OC=OM\)
Do I là tâm đường tròn ngoại tiếp ABC \(\Rightarrow IC=IA\)
\(\Rightarrow OI^2+OM^2=IA^2\Rightarrow OI^2-IA^2=-OM^2\)
Thế vào (3):
\(MA^2-MO^2-MO^2=0\Rightarrow MA=MO\sqrt{2}=\dfrac{BC\sqrt{2}}{2}\Rightarrow BC=\sqrt{2}MA\)
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 2 2022
Em vẽ hình ra được không nhỉ? Hiện tại đang không có công cụ vẽ hình nên không hình dung được dạng câu c
30 tháng 12 2021
Câu 3:
a: ĐKXĐ: \(x\ne2\)
b: \(A=\dfrac{\left(x-2\right)^2}{5\left(x-2\right)}=\dfrac{x-2}{5}\)
VN
4
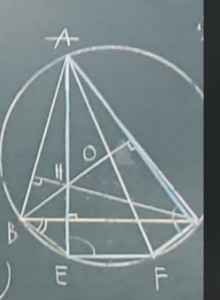
Xét đường tròn tâm O có :
góc ABF = 90 ( góc nội tiếp chắn AF) => AB vuông góc BF
ta lại có CH vuông góc AB => CH // BF (từ vuông góc đến song song)
góc ACF = 90 ( góc nội tiếp chắn AF) => AC vuông góc CF
ta lại có BH vuông góc AC => BH // CF ( từ vuông góc đến song song )
xét từ giác BHCF có
CH // BF
BH // CF
=> tg BHCF là hình bình hành ( dấu hiệu nhận biết)
mà I là tđ của đường chéo BC=> I là trnug điểm của đường chéo HF
=> H,I,F thẳng hàng