Trình bày lời giải mấy câu này giúp em với ạ!! Em xin cảm ơn.
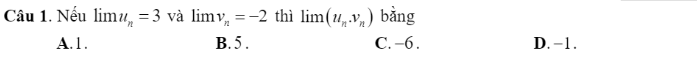



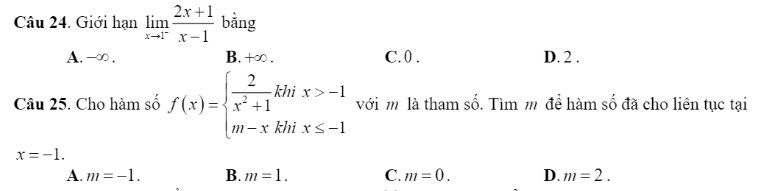

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

34:
(SBA) giao (SCD)=d đi qua S, d//AB//CD
=>d vuông góc SA,d vuông góc SD
=>(SAB;SCD)=(SA;SD)
tan ASD=AD/AS=1/căn 3
=>góc ASD=30 độ

2.B (t/c của giới hạn)
6.B H/s ko x/đ với x = 0 -> Ko liên tục tại đ x = 0
17.C
24. \(\lim\limits_{x\rightarrow\left(-1\right)^-}\dfrac{2x+1}{x+1}\) . Thấy : \(\lim\limits_{x\rightarrow\left(-1\right)^-}2x+1=2.\left(-1\right)+1=-1\)
\(\lim\limits_{x\rightarrow\left(-1\right)^-}x+1=0\) ; \(x\rightarrow\left(-1\right)^-\Rightarrow x+1< 0\).
Do đó : \(\lim\limits_{x\rightarrow\left(-1\right)^-}=+\infty\) . Chọn B
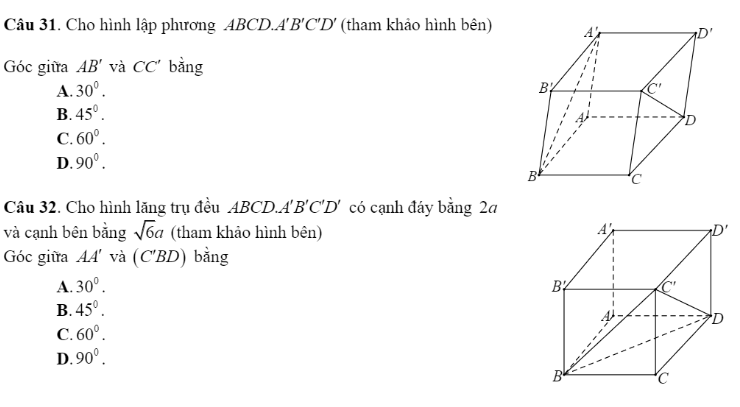
33 . B
Trên (SAB) ; Lấy H là TĐ của AB ; ta có : SH \(\perp AB\) ( \(\Delta SAB\) đều ) ; HC \(\perp AB\) ( \(\Delta ABC\) đều )
Ta có : (SAB) \(\perp\left(ABC\right)\) ; \(\left(SAB\right)\cap\left(ABC\right)=AB;SH\perp AB\)
\(\Rightarrow SH\perp\left(ABC\right)\)
\(SC\cap\left(ABC\right)=C\) . Suy ra : \(\left(SC;\left(ABC\right)\right)=\widehat{SCH}\)
Có : \(SH\perp HC\) => \(\Delta SHC\) vuông tại H
G/s \(\Delta\)ABC đều có cạnh là a \(\Rightarrow AB=a\)
\(\Delta SAB\) đều => SA = SB = AB = a
Tính được : \(SH=HC=\dfrac{\sqrt{3}}{2}a\)
\(\Delta SHC\) vuông tại H : \(tan\widehat{SCH}=\dfrac{SH}{HC}=1\)
\(\Rightarrow\widehat{SCH}=45^o\) => ...

Câu 5:
a: Xét tứ giác AHMK có
\(\widehat{AHM}=\widehat{AKM}=\widehat{KAH}=90^0\)
Do đó: AHMK là hình chữ nhật



a, cường độ dđ mạch
\(I=\dfrac{U}{R_{td}}=\dfrac{12}{10+5}=0,8\left(A\right)\)
\(\Rightarrow U_1=I.R_1=8\left(V\right)\)
\(\Rightarrow U_2=I.R_2=5.0,8=4\left(V\right)\)
b, \(\Rightarrow U_1=\dfrac{4}{2}=2\left(V\right)\)
\(I=I_2=\dfrac{4}{5}=0,8\left(A\right)\)
\(I_1=\dfrac{2}{10}=0,2\left(A\right)\)
\(I_3=I_2-I_1=0,6\left(A\right)\)
\(\Rightarrow R_3=\dfrac{U_1}{I_3}=\dfrac{2}{0,6}=\dfrac{10}{3}\left(\Omega\right)\)
1C
6D
18D
20A
24A
29A
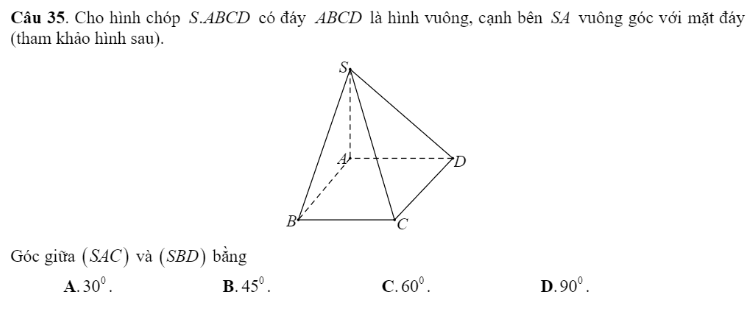
35D
31B