có bao nhiêu số nguyên dương nhỏ hơn hoặc bằng 1000, chia hết cho 7 nhưng không chia hết cho 5 và 2
mọi người giúp dùm em với ạ !
em cảm ơn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Gọi A là tập các số nguyên dương không lớn hơn 1000 chia hết cho 7,
B là tập các số nguyên dương không lớn hơn 1000 chia hết cho 11,
Khi đó A ∩ B là tập các số nguyên không lớn hơn 1000 chia hết cho 7 và chia hết cho 11,
A ∪ B là tập các số nguyên không lớn hơn 1000 chia hết cho 7 hoặc chia hết cho 11.
Trong các số nguyên dương không lớn hơn 1000 ta có:
+) 1000 7 số nguyên dương chia hết cho 7.
+) 1000 11 số nguyên dương chia hết cho 11.
+) Vì 7 và 11 là hai số nguyên tố cùng nhau nên số nguyên chia hết cho 7 và 11 là số nguyên chia hết cho (7.11). Số các số này là 1000 7 .11 .
Do đó
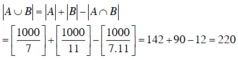

Đáp án C
Gọi A là tập các số nguyên dương không lớn hơn 1000 chia hết cho 7, B là tập các số nguyên dương không lớn hơn 1000 chia hết cho 11,
Khi đó A ∩ B là tập các số nguyên không lớn hơn 1000 chia hết cho 7 và chia hết cho 11, A ∪ B là tập các số nguyên không lớn hơn 1000 chia hết cho 7 hoặc chia hết cho 11.
Trong các số nguyên dương không lớn hơn 1000 ta có:

+) Vì 7 và 11 là hai số nguyên tố cùng nhau nên số nguyên chia hết cho 7 và 11 là số nguyên chia hết cho . Số các số này là ![]()
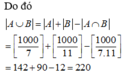

Các số chiwa hết cho 2 nhuwng không chia hết cho 5 là các số có tận cùng là 2,4,6,8
=>mỗi chục có 4 số đó
Từ 0 đến 999 có 100 chục nên ta có:
4 x 100=400(số)
Vậy nên trong các số nhỏ hơn 1000 ,có 400 số chia hết cho 2 nhưng không chia hết cho 5
#Châu's ngốc

#include <bits/stdc++.h>
using namespace std;
long long x,i,n,dem;
int main()
{
cin>>n;
dem=0;
for (i=1; i<=n; i++)
{
cin>>x;
if ((x%2==0) or (x%5==0)) dem++;
}
cout<<dem;
return 0;
}

Số chia hết cho 3 có dạng 3a ta có 0 < 3a ≤ 1000 ⇔ 0 < a < 333,3
Mà a nguyên nên có 333 số thỏa mãn
Số chia hết cho 5 có dạng 5b ta có 0 < 5b ≤ 1000 ⇔ 0 < b < 200
nên có 200 số thỏa mãn
Số chia hết cho cả 3 và 5 có dạng 15c ta có 0 < 15c ≤ 1000 ⇔ 0 < c < 66,6
nên có 66 số thỏa mãn
Do đó số các số thỏa mãn đề bài là 333 + 200 – 66 =467.
Chọn D.

Số chia hết cho 3 có dạng 3a ta có 0 < 3a ≤ 1000 ⇒ 0< a < 333,3 nên có 333 số thỏa mãn.
Số chia hết cho 5 có dạng 5b ta có 0 < 5b ≤ 1000 ⇒ 0< b < 200 nên có 200 số thỏa mãn.
Số chia hết cho cả 3 và 5 có dạng 15c ta có nên có 66 số thỏa mãn.
Do đó số các số thỏa mãn đề bài là 333 + 200 – 66 =467.
Chọn D.
Số số nguyên dương chia hết cho 7 là: \(S_1=\dfrac{994-7}{7}+1=142\)
Số số vừa chia hết cho 7 vừa chia hết cho 5 (nghĩa là chia hết 35): \(S_2=\dfrac{980-35}{35}+1=28\)
Số số vừa chia hết cho 7 vừa chia hết cho 2: \(S_3=\dfrac{994-14}{14}+1=71\)
Số số chia hết cho cả 7;2;5 là: \(S_4=\dfrac{980-70}{70}+1=14\)
Số số thỏa mãn yêu cầu đề bài: \(S_1+S_4-\left(S_2+S_3\right)=57\)