Ét O Ét, giúp e bagi 6 với 🙏🙏🙏🙏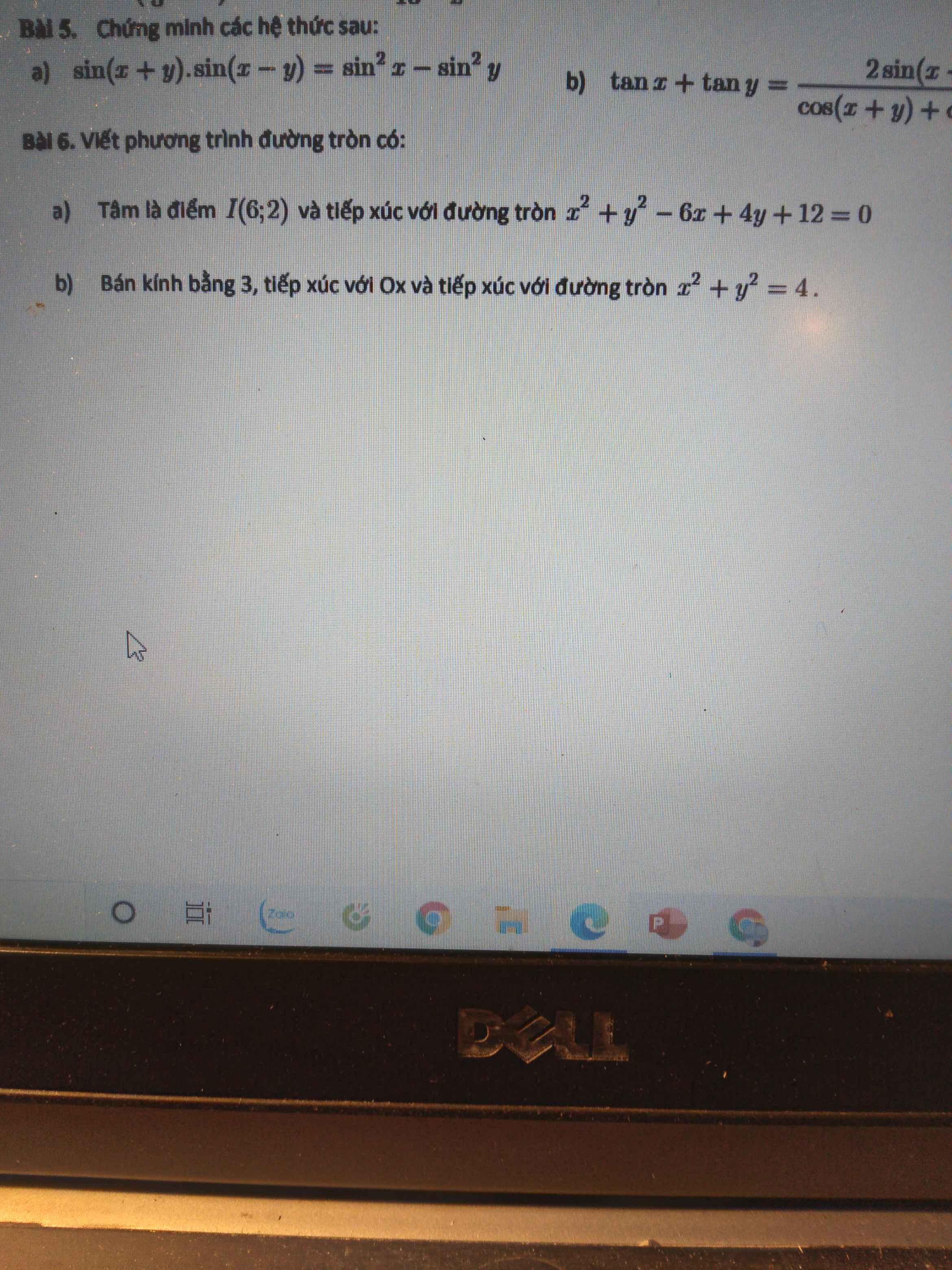
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 7 2023
4:
a: -90<a<0
=>cos a>0
cos^2a=1-(-4/5)^2=9/25
=>cosa=3/5
\(sin\left(45-a\right)=sin45\cdot cosa-cos45\cdot sina=\dfrac{\sqrt{2}}{2}\left(cosa-sina\right)\)
\(=\dfrac{\sqrt{2}}{2}\left(\dfrac{3}{5}-\dfrac{4}{5}\right)=\dfrac{-\sqrt{2}}{10}\)
b: pi/2<a<pi
=>cosa<0
cos^2a+sin^2a=0
=>cos^2a=16/25
=>cosa=-4/5
tan a=3/5:(-4/5)=-3/4
\(tan\left(a+\dfrac{pi}{3}\right)=\dfrac{tana+\dfrac{tanpi}{3}}{1-tana\cdot tan\left(\dfrac{pi}{3}\right)}\)
\(=\dfrac{-\dfrac{3}{4}+\sqrt{3}}{1-\dfrac{-3}{4}\cdot\sqrt{3}}=\dfrac{48-25\sqrt{3}}{11}\)
c: 3/2pi<a<pi
=>cosa>0
cos^2a+sin^2a=1
=>cos^2a=25/169
=>cosa=5/13
cos(pi/3-a)
\(=cos\left(\dfrac{pi}{3}\right)\cdot cosa+sin\left(\dfrac{pi}{3}\right)\cdot sina\)
\(=\dfrac{5}{13}\cdot\dfrac{1}{2}+\dfrac{-12}{13}\cdot\dfrac{\sqrt{3}}{2}=\dfrac{5-12\sqrt{3}}{26}\)
TM
28 tháng 12 2022
Quy trình giâm cành ở cây khoai lang :
bước 1 : Chuẩn bị đất trồng cây khoai lang.
bước 2 : Chuẩn bị cành giâm của cây khoai lang.
bước 3 : Giâm cành cây khoai lang vào đất trồng.
bước 4 : Chăm sóc cành giâm.
N
13 tháng 1 2022
Do vị trí địa lí nằm án ngữ trên con đường hàng hải nối liền giữa Ấn Độ Dương với Thái Bình Dương, từ lâu khu vực Đông Nam Á vẫn được coi là cầu nối giữa Trung Quốc, Nhật Bản với Ấn Độ, Tây Á và Địa Trung Hải.
Đông Nam Á bao gồm hai khu vực riêng biệt là Đông Nam Á lục địa và Đông Nam Á hải đảo; lại nằm trong vùng nhiệt đới gió mùa, có lượng mưa lớn nên rất thích hợp cho sự phát triển của cây lúa nước và nhiều cây trồng khác. Nơi đây được biết đến là “cái nôi” của nền văn minh lúa nước và là quê hương của nhiều loại cây gia vị, hương liệu nổi tiếng.
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 3 2022
a.
Đường tròn có tâm \(\left\{{}\begin{matrix}x_I=2m\\y_I=-m-3\end{matrix}\right.\)
\(\Rightarrow x_I+2y_I=2m+2\left(-m-3\right)=-6\)
\(\Leftrightarrow x_I+2y_I+6=0\)
Hay quỹ tích tâm I của đường tròn là đường thẳng có pt: \(x+2y+6=0\)
b.
Gọi H là trung điểm AB \(\Rightarrow\left\{{}\begin{matrix}AH=\dfrac{1}{2}AB=3\\IH\perp AB\end{matrix}\right.\) \(\Rightarrow IH=d\left(I;d\right)\)
\(R=IA=\sqrt{\left(2m\right)^2+\left(-m-3\right)^2-\left(5m^2-6m-16\right)}=5\)
\(\Rightarrow IH=\sqrt{IA^2-AH^2}=4\)
\(d\left(I;d\right)=\dfrac{\left|3.2m-4\left(-m-3\right)+12\right|}{\sqrt{3^2+\left(-4\right)^2}}=4\)
\(\Leftrightarrow\left|10m+24\right|=20\Rightarrow\left[{}\begin{matrix}m=-\dfrac{2}{5}\\m=-\dfrac{22}{5}\end{matrix}\right.\)
Giúp em với ạ 🙏🙏🙏🙏🙏🙏
24 tháng 2 2022
Câu 27.
Cơ năng vật:
\(W=\dfrac{1}{2}mv^2+mgz=\dfrac{1}{2}\cdot5\cdot10^2+5\cdot10\cdot30=1750J\)
Câu 28.
\(m=200tấn=2\cdot10^5kg\)
\(z=12km=12000m\)
\(v=720\)km/h=200m/s
Cơ năng vật:
\(W=\dfrac{1}{2}mv^2+mgz=\dfrac{1}{2}\cdot2\cdot10^5\cdot200^2+2\cdot10^5\cdot10\cdot12000=2,8\cdot10^{10}J\)
24 tháng 2 2022
Câu 29.
a)Cơ năng vật ban đầu:
\(W=W_t=mgz=2\cdot10\cdot30=600J\)
b)Vận tốc vật khi sắp chạm đất:
\(v=\sqrt{2gh}=\sqrt{2\cdot10\cdot30}=10\sqrt{6}\)m/s
c)Tại nơi có động năng bằng thế năng.
\(W_1=W_đ+W_t=2W_t=2mgz_1\)
Bảo toàn cơ năng: \(W=W_1\)
\(\Rightarrow600=2mgz_1\)
\(\Rightarrow z_1=\dfrac{600}{2\cdot2\cdot10}=15m\)
d)Tại nơi \(W_đ=2W_t\)
Cơ năng vật: \(W_2=3W_t=3mgz_2\)
Bảo toàn cơ năng: \(W=W_2\)
\(\Rightarrow600=3mgz_2\)
\(\Rightarrow z_2=\dfrac{600}{3\cdot2\cdot10}=10m\)
Giúp em với ạ 🙏🙏🙏🙏🙏
24 tháng 2 2022
Câu 32.
a)Độ cao mặt phẳng nghiêng:
\(h=l\cdot sin\alpha=10sin30^o=5m\)
Bảo toàn cơ năng: \(W_đ=W_t\)
\(\Rightarrow\dfrac{1}{2}mv^2=mgh\)
\(\Rightarrow v=\sqrt{2gh}=\sqrt{2\cdot10\cdot5}=10\)m/s
b)Chọn mốc thế năng tại chân mặt phẳng gnhieeng.
Lực ma sát:
\(F_{ms}=\mu N=\mu\cdot mgcos\alpha=0,2\cdot m\cdot10\cdot cos30^o=\sqrt{3}m\left(N\right)\)
Cơ năng vật khi ở đỉnh mặt phẳng nghiêng:
\(W_1=mgh=m\cdot10\cdot5=50m\left(J\right)\)
Cơ năng vật khi ở chân mặt phẳng nghiêng:
\(W_2=\dfrac{1}{2}mv^2\left(J\right)\)
Công lực ma sát: \(A_{ms}=F_{ms}\cdot s=\sqrt{3}m\cdot5=5\sqrt{3}m\left(J\right)\)
Bảo toàn cơ năng:
\(W_2-W_1=A_{ms}\)
\(\Rightarrow\dfrac{1}{2}mv^2-50m=5\sqrt{3}m\)
\(\Rightarrow v=10,83\)m/s
24 tháng 2 2022
Câu 31.
a)Độ cao cực đại.
Bảo toàn cơ năng: \(W=W_đ=W_t\)
\(\Rightarrow\dfrac{1}{2}mv^2=mgh_{max}\)
\(\Rightarrow h_{max}=\dfrac{v^2}{2g}=\dfrac{7^2}{2\cdot10}=2,45m\)
b)Ở độ cao thế năng gấp 4 lần động năng.
\(W_2=W_đ+W_t=5W_t=5mgz\)
Bảo toàn cơ năng: \(W=W_2\)
\(\Rightarrow\dfrac{1}{2}mv^2=5mgz\)
\(\Rightarrow\dfrac{1}{2}\cdot7^2=5\cdot10\cdot z\)
\(\Rightarrow z=0,49m\)
Giúp em với ạ 🙏🙏🙏🙏🙏
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 4 2022
4b.
\(\dfrac{\pi}{2}< a< \pi\Rightarrow cosa< 0\Rightarrow cosa=-\sqrt{1-sin^2a}=-\dfrac{4}{5}\)
\(\Rightarrow tana=\dfrac{sina}{cosa}=-\dfrac{3}{4}\)
\(tan\left(a+\dfrac{\pi}{3}\right)=\dfrac{tana+tan\left(\dfrac{\pi}{3}\right)}{1-tana.tan\left(\dfrac{\pi}{3}\right)}=\dfrac{-\dfrac{3}{4}+\sqrt{3}}{1-\left(-\dfrac{3}{4}\right).\sqrt{3}}=...\)
c.
\(\dfrac{3\pi}{2}< a< 2\pi\Rightarrow cosa>0\Rightarrow cosa=\sqrt{1-sin^2a}=\dfrac{5}{13}\)
\(cos\left(\dfrac{\pi}{3}-a\right)=cos\left(\dfrac{\pi}{3}\right).cosa+sin\left(\dfrac{\pi}{3}\right).sina=\dfrac{1}{2}.\dfrac{5}{13}+\left(-\dfrac{12}{13}\right).\dfrac{\sqrt{3}}{2}=...\)
a.
Đường tròn (C): \(x^2+y^2-6x+4y+12=0\) có tâm \(J\left(3;-2\right)\) bán kính \(r=1\)
Tiếp điểm A của 2 đường tròn phải nằm trên đường nối tâm IJ
\(\overrightarrow{JI}=\left(3;4\right)\Rightarrow\) phương trình IJ có dạng:
\(4\left(x-3\right)-3\left(y+2\right)=0\Leftrightarrow4x-3y-18=0\)
Tọa độ tiếp điểm A là nghiệm của hệ :
\(\left\{{}\begin{matrix}4x-3y-18=0\\x^2+y^2-6x+4y+12=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{4x-18}{3}\\x^2+y^2-6x+4y+12=0\end{matrix}\right.\)
\(\Rightarrow x^2+\left(\dfrac{4x-18}{3}\right)^2-6x+4\left(\dfrac{4x-18}{3}\right)+12=0\)
\(\Rightarrow\dfrac{25}{9}x^2-\dfrac{50}{3}x+24=0\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{12}{5}\Rightarrow y=-\dfrac{14}{5}\\x=\dfrac{18}{5}\Rightarrow y=-\dfrac{6}{5}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}A\left(\dfrac{12}{5};-\dfrac{14}{5}\right)\\A\left(\dfrac{18}{5};-\dfrac{6}{5}\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\overrightarrow{AI}=\left(\dfrac{18}{5};\dfrac{24}{5}\right)\\\overrightarrow{AI}=\left(\dfrac{12}{5};\dfrac{16}{5}\right)\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}R^2=AI^2=36\\R^2=AI^2=\dfrac{36}{5}\end{matrix}\right.\)
Có 2 đường tròn thỏa mãn:
\(\left[{}\begin{matrix}\left(x-6\right)^2+\left(y-2\right)^2=36\\\left(x-6\right)^2+\left(y-2\right)^2=\dfrac{36}{5}\end{matrix}\right.\)
b.
Đường tròn (C): \(x^2+y^2=4\) có tâm \(O\left(0;0\right)\) và bán kính \(r=2\)
Gọi \(I\left(a;b\right)\) là tâm của đường tròn (C') cần tìm
Do (C') tiếp xúc Ox \(\Rightarrow d\left(I;Ox\right)=3\Rightarrow\dfrac{\left|b\right|}{1}=3\Rightarrow b=\pm3\)
TH1: \(I\left(a;3\right)\Rightarrow\overrightarrow{OI}=\left(a;3\right)\Rightarrow OI=\sqrt{a^2+9}\)
Do 2 đường tròn tiếp xúc \(\Rightarrow\left[{}\begin{matrix}R+r=OI\\R-r=OI\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}OI=5\\OI=1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\sqrt{a^2+9}=5\\\sqrt{a^2+9}=1\left(vn\right)\end{matrix}\right.\)
\(\Rightarrow a=\pm4\)
TH2: hoàn toàn tương tự ta có tìm được \(a=\pm4\)
Vậy có 4 đường tròn thỏa mãn: \(\left[{}\begin{matrix}\left(x-4\right)^2+\left(y-3\right)^2=9\\\left(x+4\right)^2+\left(y-3\right)^2=9\\\left(x-4\right)^2+\left(y+3\right)^2=9\\\left(x+4\right)^2+\left(y+3\right)^2=9\end{matrix}\right.\)