Cho tam giác ABC nhọn . Trên tia đối của tia AB lấy điểm D sao cho AD=AB. Trên tia đối của AC lấy điểm E sao cho AE=AC.
1) So sánh BC và DE.
2) AH và AK lần lượt là đường cao của tam giác ABC và ADE. Chứng minh H, A, K thẳng hàng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 10 2021
Xét tứ giác EDCB có
A là trung điểm của đường chéo DB
A là trung điểm của đường chéo EC
Do đó: EDCB là hình bình hành
Suy ra: ED//BC
hay \(\widehat{ADE}=\widehat{ABC};\widehat{AED}=\widehat{ACB}\)
14 tháng 4 2021
1) Xét ΔCAB vuông tại A và ΔEAD vuông tại A có
AB=AD(gt)
AC=AE(gt)
Do đó: ΔCAB=ΔEAD(hai cạnh góc vuông)
Suy ra: BC=DE(hai cạnh tương ứng)
14 tháng 4 2021
2) Xét ΔABD có AB=AD(gt)
nên ΔABD cân tại A(Định nghĩa tam giác cân)
Xét ΔABD cân tại A có \(\widehat{BAD}=90^0\)(gt)
nên ΔABD vuông cân tại A(Định nghĩa tam giác vuông cân)
22 tháng 1
a: Xét ΔABC vuông tại A và ΔADE vuông tại A có
AB=AD
AC=AE
Do đó: ΔABC=ΔADE
=>BC=DE
b: Xét ΔABD vuông tại A có AB=AD
nên ΔABD vuông cân tại A
=>\(\widehat{ABD}=\widehat{ADB}=45^0\)
Xét ΔAEC vuông tại A có AE=AC
nên ΔAEC vuông cân tại A
=>\(\widehat{AEC}=\widehat{ACE}=45^0\)
Ta có: \(\widehat{ABD}=\widehat{AEC}\left(=45^0\right)\)
mà hai góc này là hai góc ở vị trí so le trong
nên BD//CE
10 tháng 12 2021
a: Xét ΔABC vuông tại A và ΔADE vuông tại A có
AB=AD
AC=AE
Do đó: ΔABC=ΔADE
24 tháng 9 2022
a: Xét ΔABC vuông tại A và ΔADE vuông tại A có
AB=AD
AC=AE
Do đó: ΔABC=ΔADE
b: AM=ED/2
AN=BC/2
mà ED=BC
nên AM=AN
6 tháng 1 2022
a: Xét ΔEAD và ΔBAC có
AE=AB
\(\widehat{EAD}=\widehat{BAC}\)
AD=AC
Do đó: ΔEAD=ΔBAC
Suy ra: ED=BC
b: Xét ΔACD có AC=AD
nên ΔACD cân tại A
Xét ΔABE có AB=AE
nên ΔABE cân tại A
1 tháng 7 2023
a: Xét ΔABD có
AI vừa là đường cao, vừa là trung tuyến
=>ΔABD cân tại A
b: Xét ΔAHI vuông tại H và ΔAKI vuông tại K có
AI chung
góc HAI=góc KAI
=>ΔAHI=ΔAKI
=>HI=KI
c: HI=KI
KI<ID
=>HI<ID
14 tháng 4 2022
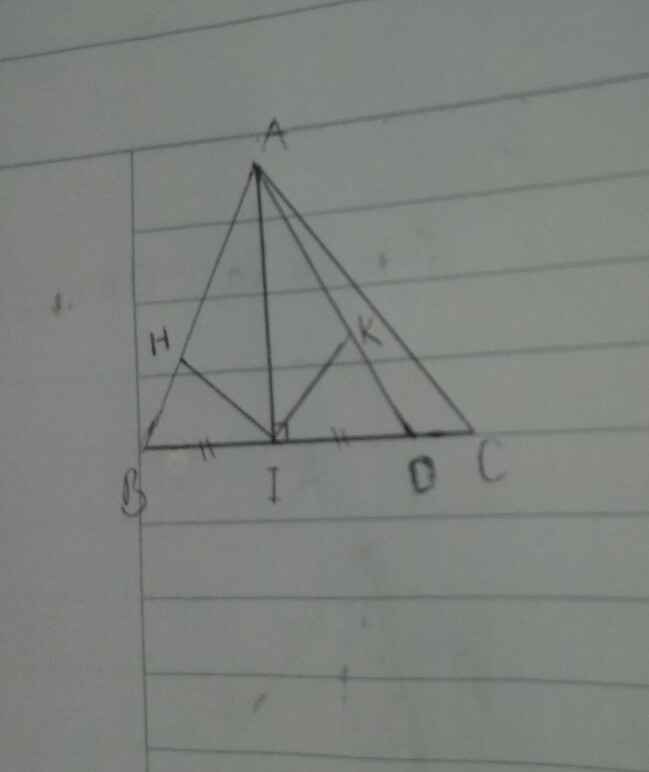
rồi từ câu a) là sai đề nhaaaa em ( ko thể chứng minh đc - do AB < AC < BC)
1: Xét tứ giác BCDE có
A là trung điểm của BD
A là trung điểm của CE
Do đó; BCDE là hình bình hành
Suy ra: BC//DE
2: AH\(\perp\)BC
mà BC//DE
nên \(AH\perp\)DE
mà AK\(\perp\)DE
và AH,AK có điểm chung là A
nên H,A,K thẳng hàng
Em cảm ơn ạ