Cho ABC vuông cân tại A, BC = 3cm. Vẽ ACE vuông cân tại E (E và B nằm khác phía đối với AC). CMR:
a, AECB là hình thang vuông
b, Tính các góc và các cạnh của hình thang đó
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
T
24 tháng 5 2016
bai lam: vi tam giac abc vuong tai a suy ra bac=45 (1)
vi tam giac ace vuong tai e suy ra ace=45 (2)
bce=bac+ace (3)
tu 1 2 3 suy ra bce=aec (ma 2 goc o vi tri trong cung phia phu nhau) suy ra ae//bc nen tu giac aecb la hinh thang co aec =90 nen aecb la hinh thang vuong
tinh gum minh cac ban nha?
TT
11 tháng 8 2016
Bài mình làm cực chi tiết nên có một số chỗ viết tắt: gt:giả thiết, dhnb:dấu hiệu nhận biết, đ/n:định nghĩa, cmt:chứng minh trên, t/c: tính chất
a) Vì tam giác ABC vuông cân ở A (gt)=> góc ACB=45 độ.
tam giác ACE vuông cân ở E (gt)=> góc EAC=45 độ.
mà góc EAC và góc ACB ở vị trí so le trong.
Từ 3 điều trên=> AE//BC (dhnb) => AECB là hình thang (đ/n) mà góc AEC=90 độ (tam giác ACE vuông cân) => AECB là hình thang vuông.
b) Vì AECB là hình thàng vuông(cmt) mà góc AEC= 90 độ (tam giác ACE vuông cân). => góc ACE=90 độ.
Có: góc ABC= 45 độ (cmt).
tam giác AEC vuông cân ở E (gt)=> góc EAC=45 độ (t/c) mà góc BAC+ góc EAC= góc BAE và góc BAC= 90 độ (tam giác BAC vuông cân)=> góc BAE= 90 độ=45 độ= 135 độ.
Gọi AD là đường trung trực tam giác ABC=> AD=BD=BC=1/2BC=1/2*2=1 cm (chỗ này là tính chất tam giác vuông: trung tuyến ứng với cạnh huyền thì bằng nửa cạnh huyền nhé). [đây là điều thứ nhất suy ra được]
=> AD vông góc với BC. [đây là điều thứu hai suy ra được]
Xét tam giác ADC vuông tại D (AD vuông góc BC) và tam giác AEC vuông tại E (gt) có: Cạnh huyền AC chung. Góc EAC= góc BCA (cmt) => tam giác ADC= tam giác CEA (ch-gn) => AD= EC ( 2 cạnh tương ứng) mà AD=1cm(cmt) => AE=1cm.
Xét tam giác ADB vuông (AD vuông góc BC) có: AD2+ BD2 = AB2 ( định lí Pytago)
12 + 12 =AB2 => 1+1=AB2 => Ab bằng căn bậc hai cm.
19 tháng 8 2018
* Vì tam giác ABcCvuông cân tại A suy ra: A1=C1=45 độ
* Vì tam giác AEC vuông cân tại E suy ra: A2=C2=45 độ
* Có: C1=A2 (=45 độ) (1)
C1 va A2 ở vị trí so le trong (2)
Từ (1) và (2) suy ra: AE//BC
* Tứ giác ABCE có: AE//BC (cmt)
E=90 độ
su ra ABCE là hình thang vuông.
* Áp dụng định lí Py-ta-go vào tam giác ABC vuông cân tại A ta được:
AB^2+AC^2=BC^2
suy ra: 2AB^2=2^2
suy ra: 2AB^2=4
suy ra: AB^2=4:2=2
suy ra: AB= căn 2 cm
suy ra AB=AC=căn 2 cm (do tam giác ABC vuông cân ở A)
* Áp dụng định lí Py-ta-go vào tam giác ACE vuông căn tại E ta được:
AE^2+EC^2=AC^2
suy ra: 2AE^2= căn 2^2
suy ra: 2AE^2=2
Tính các góc thì chỉ cần việc cộng vào thôi. Bn tự tính nhé.
suy ra: AE^2=2:2=1(cm)
suy ra: AE= 1cm
suy ra AE=EC=1cm (do tam giác AEC vuông cân ở E)
CM
26 tháng 1 2018
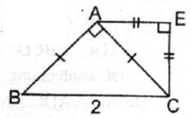
∠ E = ∠ (ECB) = 90 0 , ∠ B = 45 0
∠ B + ∠ (EAB) = 180 0 (hai góc trong cùng phía bù nhau)
⇒ ∠ (EAB) = 180 0 - ∠ B = 180 0 – 45 0 = 135 0
Tam giác ABC vuông tại A. Theo định lí Py-ta-go ta có:
A B 2 + A C 2 = B C 2 mà AB = AC (gt)
⇒ 2 A B 2 = B C 2 = 2 2 = 4
A B 2 = 2 ⇒ AB= √2(cm) ⇒ AC = √2 (cm)
Tam giác AEC vuông tại E. Theo định lí Py-ta-go ta có:
E A 2 + E C 2 = A C 2 , mà EA = EC (gt)
⇒ 2 E A 2 = A C 2 = 2
E A 2 = 1
⇒ EA = 1(cm) ⇒ EC = 1(cm)
a, Có tam giác ABC vuông cân tại A (gt)
=> \(\widehat{ABC}=\widehat{ACB}=45^o\)
Có tam giác ACE vuông cân tại E (gt)
=> \(\widehat{EAC}=\widehat{ECA}=45^o\)và \(\widehat{AEC}=90^o\)
Mà \(\widehat{ECA}+\widehat{ACB}=\widehat{ECB}\)
=> \(\widehat{ECB}=90^o\)
=> góc AEC + góc ECB = 180o
Mà 2 góc này ở vị trí trong cùng phía
=> AE // BC
=> Tứ giác AECB là hình thang có \(\widehat{AEC}=90^o\)
=> Hình thang AECB là hình thang vuông (Đpcm)
b, (tiếp lỡ ấn nhầm nút gửi câu trả lời ~~~~)
Kẻ AM vuông góc BC
Mà tam giác ABC vuông cân tại A
=> AM là trung tuyến tam giác ABC
=> AM = BM = CM = \(\frac{1}{2}\)BC (trung tuyến ứng vs cạnh huyền bằng nửa cạnh huyền)
=> AM = BM = CM = 1,5 cm
Xét tam giác AMB vuông tại M
=> AM2 + BM2 = AB2 (Pitago)
=> (1,5)2 + (1,5)2 = AB2
=> AB2 = 4,5
=> AB = \(\sqrt{4,5}\)cm
Mà AB = AC (tam giác ABC vuông cân tại A)
=> AC = \(\sqrt{4,5}\)cm
Có: tam giác AEC vuông cân tại E (gt)
=> EA = EC
=> EA2 + EC2 = AC2
=> 2.EA2 = 2.EC2 = 4,5
=> EA2 = EC2 = 2,25
=> EA = EC = 1,5
=> Các cạnh của hình thang là:
AB = \(\sqrt{4,5}\)cm
AE = EC = 1,5 cm
BC = 3cm