Jup mình với ạ mai mình nộp mất rùiii ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NN
0
31 tháng 10 2021
Bạn ơi, làm như vậy thì quá ngắn rồi ạ, với lại bạn làm thiếu mất đề bài của mình rồi
KV
29 tháng 10 2023
1) 43 . 78 - 43 . 48 + 30 . 80 - 30 . 23
= 43.(78 - 48) + 30.(80 - 23)
= 43.30 + 30.57
= 30.(43 + 57)
= 30.100
= 3000
2) 31.175 - 31.50 + 69.125
= 31.(175 - 50) + 69.125
= 31.125 + 69.125
= 125.(31 + 69)
= 125.100
= 12500
3) 2.[(7 - 3¹³ : 3¹²) : 2² + 99] - 10²
= 2.[(7 - 3) : 4 + 99] - 100
= 2.(4 : 4 + 99) - 100
= 2.(1 + 99) - 100
= 2.100 - 100
= 200 - 100
= 100
4) 2²⁰¹⁹.2² : 2²⁰¹⁶ - 125 : 5² + 2019⁰
= 2²⁰²¹ : 2²⁰¹⁶ - 125 : 25 + 1
= 2⁵ - 5 + 1
= 32 - 4
= 28
NN
1
23 tháng 11 2021
A B C D M N XXét tứ giác AMDN có ^AMD=^MAN=^AND=90∞
⇒AMDN là hình chữ nhật
hcn AMDN có AD là phân giác góc A
⇒AMDN là hình vuông(dấu hiệu 3)
7 tháng 3 2022
\(\left\{{}\begin{matrix}2x+y=1\\x+y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\x+y=-1\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}x=2\\y=-3\end{matrix}\right.\)
\(\left\{{}\begin{matrix}2x+2y=18\\x-y=-6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+y=9\\x-y=-6\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}2x=3\\x-y=-6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{2}\\y=\dfrac{15}{2}\end{matrix}\right.\)\(\left\{{}\begin{matrix}2x+3y=6\\x-2y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x+6y=12\\3x-6y=9\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}7x=21\\3x-6y=9\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}x=3\\y=0\end{matrix}\right.\)
HT
1
NV
Nguyễn Việt Lâm
Giáo viên
3 tháng 5 2021
Phương trình (D) có dạng:
\(y=k\left(x-1\right)-2\Leftrightarrow y=kx-k-2\)
Phương trình hoành độ giao điểm (P) và (D):
\(-\dfrac{x^2}{4}=kx-k-2\Leftrightarrow x^2+4kx-4\left(k+2\right)=0\) (1)
\(\Delta'=4k^2+4\left(k+2\right)=\left(2k+1\right)^2+7>0\) ; \(\forall k\)
\(\Rightarrow\) (1) luôn có 2 nghiệm pb hay (D) luôn cắt (P) tại 2 điểm pb A và B
b. Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_A+x_B=-4k\\x_Ax_B=-4\left(k+2\right)\end{matrix}\right.\)
Đặt \(A=x_A^2x_B+x_Ax_B^2=x_Ax_B\left(x_A+x_B\right)\)
\(A=-4\left(k+2\right).\left(-4k\right)=16\left(k^2+2k\right)=16\left(k+1\right)^2-16\ge-16\)
\(\Rightarrow A_{min}=-16\) khi \(k+1=0\Leftrightarrow k=-1\)
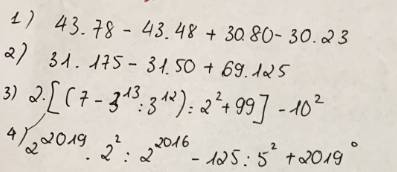
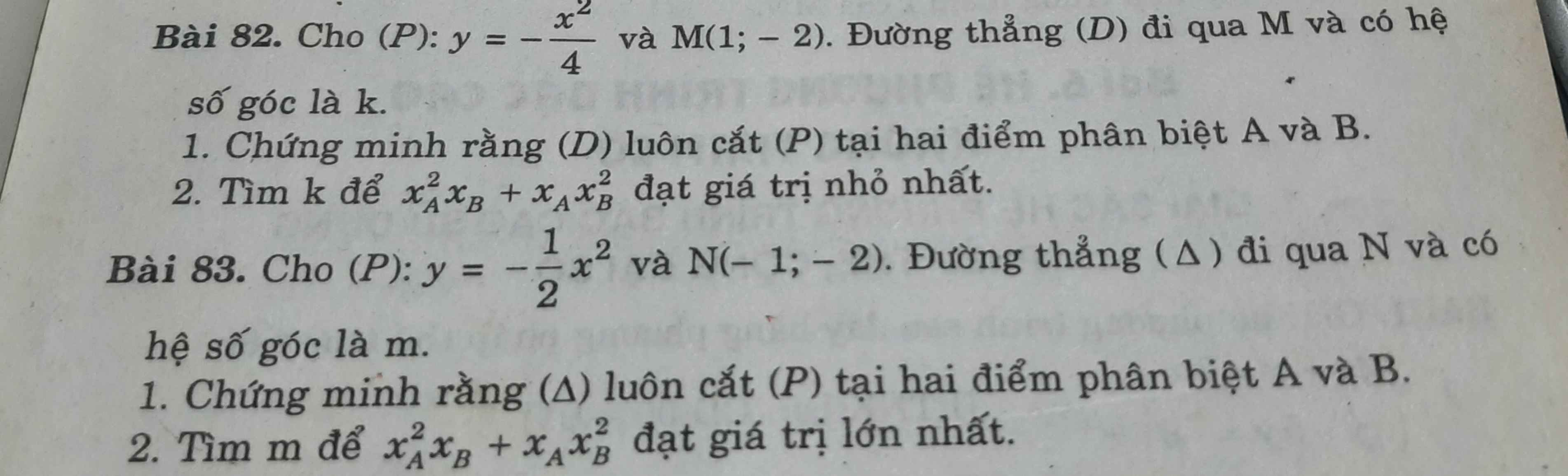
4:
a: góc BFC=góc BEC=90 độ
=>BFEC nội tiếp
b: Kẻ tiếp tuyến Ax của (O)
=>góc xAC=góc ABC
=>góc xAC=góc AEF
=>Ax//EF
=>OA vuông góc EF
ME=MF
IF=IE
=>MI là trung trực của EF
=>MI vuông góc EF
=>MI//OA