Từ các chữ số 1,2,3,...,7 lập hai số a&b có 7 chữ số, mỗi chữ số chỉ được viết một lần. Chứng minh a không chia hết cho b.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn D
Gọi số tự nhiên có chữ số khác nhau lấy từ các phần tử của tập A là ![]()
![]()
+) Chọn a có 6 cách.
+) Chọn bốn chữ số b,c,d,e có A 6 4 cách.
Vậy số cách lập số tự nhiên có 5 chữ số khác nhau lấy từ các phần tử của tập A là
6.
A
6
4
= 2160 cách. Do đó số phần tử của không gian mẫu là ![]()
Gọi biến cố B: ‘‘Số tự nhiên lập được chia hết cho 5 và các chữ số 1,2,3 luôn có mặt cạnh nhau’’.
TH1: Số lập được có dạng a b c d 0 ¯
+) Vì các chữ số 1,2,3 luôn có mặt cạnh nhau nên ta coi ba số đó là khối X. Xếp ba số 1,2,3 trong khối X có P 3 cách.
+) Chọn 1 số trong tập ![]()
+) Xếp khối X và số vừa chọn vào vị trí có P 2 cách.
Theo quy tắc nhân ta có P 3 .3 P 2 = 36 số.
TH2: Số lập được có dạng a b c 05 ¯
+) Vì các chữ số 1,2,3 luôn có mặt cạnh nhau nên ta có P 3 cách chọn số a,b,c
Vậy có P 3 = 6 số.
TH3: Số lập được có dạng ![]()
+) Vì các chữ số 1,2,3 luôn có mặt cạnh nhau nên ta coi ba số đó là khối X. Xếp ba số 1,2,3 trong khối X có P 3 cách.
+) Chọn số trong tập {4;6} có C 2 1 = 2 cách.
+) Xếp khối X và số vừa chọn vào vị trí có P 2 cách.
Theo quy tắc nhân ta có P 3 .2 P 2 = 24 số.
Vậy số kết quả xảy ra của biến cố B là ![]()
Xác suất của biến cố B là 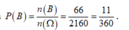

Chọn B
Gọi số cần tìm có dạng là ![]()
Mỗi bộ ba số ![]() là một chỉnh hợp chập 3 của 9 phần tử.
là một chỉnh hợp chập 3 của 9 phần tử.
Vậy số các số cần tìm là A 9 3 số.

Chọn B
Lấy ra 3 chữ số từ 9 chữ số và sắp xếp 3 chữ số đó theo thứ tự, mỗi cách sắp xếp tạo nên 1 số có 3 chữ số khác nhau. Như vậy, có A 9 3 số cần tìm.
* Nhận xét: Mục đích bài toán là phân biệt hai khái niệm: Chỉnh hợp và tổ hợp. Học sinh có thể giải bài này bằng phương pháp nhân: 9.8.7, và so sánh với 4 đáp án. Hai chỉnh hợp khác nhau thì có thể khác nhau về phần tử hoặc khác nhau về thứ tự các phần tử. Hai tổ hợp khác nhau thì khác nhau về phần tử.
*Lý thuyết Chỉnh hợp
- Cho tập hợp A có n phần tử và cho số nguyên k, (1 ≤ k ≤ n). Khi lấy k phần tử của A và sắp xếp chúng theo một thứ tự, ta được một chỉnh hợp chập k của n phần tử của A (gọi tắt là một chỉnh hợp n chập k của A).
- Số các chỉnh hợp chập k của một tập hợp có n phần tử là: 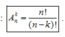
- Một số qui ước: ![]()
*Lý thuyết Tổ hợp
- Cho tập hợp A có n phần tử và cho số nguyên k, (1 ≤ k ≤ n). Mỗi tập hợp con của A có phần tử được gọi là một tổ hợp chập k của n phần tử của A.
- Số các chỉnh hợp chập k của một tập hợp có n phần tử là : 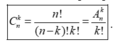
- Một số quy ước: ![]() với qui ước này ta có
với qui ước này ta có 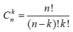 đúng với số nguyên dương k, thỏa 0
≤
k
≤
n
đúng với số nguyên dương k, thỏa 0
≤
k
≤
n
PT 14.1. Chọn B
TH1 ![]()
TH2: ![]() vì
vì ![]()
Như vậy, có ![]() số cần tìm
số cần tìm
PT 14.2.
Chọn C
Mỗi tập con có 3 phần tử thuộc tập {1,2,...,9} xác định duy nhất một số có 3 chữ số tăng dần từ trái qua phải (đảm bảo chữ số đầu tiên khác 0).
Mỗi tập con có 3 phần tử thuộc tập {0,1,2....,9} xác định duy nhất một số có 3 chữ số giảm dần từ trái qua phải.
Như vậy, có ![]() số cần tìm.
số cần tìm.

Để lập được một số có 3 chữ số từ các số 1, 2, 3, .., 9, ta cần chọn 3 số từ tập các số trên và sắp xếp chúng theo một thứ tự cụ thể.
Số cách chọn 3 số từ 9 số là: C(9,3) = 84
Mỗi cách chọn 3 số đều có thể sắp xếp thành một số có 3 chữ số, do đó số lượng số có 3 chữ số từ các số 1,2,3,..,9 là 84 x 3! = 504.
Vậy có thể lập được 504 số có 3 chữ số từ các số 1, 2, 3, .., 9.

tìm số có 2 chữ số biết số đó chia cho 2 dư 1 , chia hết cho 3 , chia cho 5 dư 2

Vì 1 + 2 + 3 ⋮ 3 nên ta có "
+) 3 cách chọn chữ số hàng trăm
+) 2 cách chọn chữ số hàng chục
+) 1 cách chọn chữ số hàng đơn vị
=> Lập được tất cả các số chia hết cho 3 từ các số 1 ; 2 và 3 là :
3 x 2 x 1 = 6 ( số )
Đáp số : với các số 1 ; 2 ; 3 thì ta lập được 6 số có 3 chữ số chia hết cho 3
~~Học tốt~~

có các số: 12,13,21,23,31,32
tổng của chúng là:
12+13+21+23+31+32=132
kick mik nhé bạn