Cho đường tròn (O) và hai điểm A, B nằm bên ngoài đường tròn. Dựng đường kính COD sao cho AC=BD.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
3 tháng 10 2019
* Cách dựng
- Dựng A’ đối xứng với A qua tâm O của đường tròn
- Dựng đường thẳng x là trung trực của A’B
- Gọi giao điểm của đường thẳng x và đường tròn (O) là D
- Dựng đường kính COD
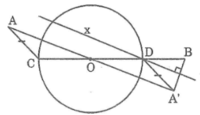
* Chứng minh
Ta có: OA = OA’ và OD = OC
Suy ra tứ giác ACA’D là hình bình hành
Suy ra: AC = A’D
Lại có: A’D = BD (tính chất đường trung trực)
Suy ra: AC = BD
23 tháng 6 2017
Biện luận :
Tùy theo số giao điểm của d và đường tròn (O) là 2, 1, 0 mà bài toán có 2, 1, 0 nghiệm hình.
(Trên hình 89, bài toán có 2 nghiệm hình)
CM
18 tháng 11 2018
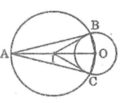
* Phân tích
Giả sử tiếp tuyến AB và AC cần dựng thỏa mãn điều kiện bài toán
Ta có: AB ⊥ OB ⇒ ∠ ABO = 90 °
AC ⊥ OC ⇒ ∠ ACO = 90 °
Tam giác ABO có ∠ ABO = 90 ° nội tiếp trong đường tròn đường kính AO và tam giác ACO có ∠ ACO = 90o nội tiếp trong đường tròn đường kính AO.
Suy ra B và C là giao điểm của đường tròn đường kính AO với đường tròn (O).
* Cách dựng
- Dựng I là trung điểm của OA
- Dựng đường tròn (I; IO) cắt đường tròn (O) tại B và C
- Nối AB, AC ta được hai tiếp tuyến cần dựng
* Chứng minh
Tam giác ABO nội tiếp trong đường tròn (I) có OA là đường kính nên: ∠ ABO = 90 °
Suy ra: AB ⊥ OB tại B nên AB là tiếp tuyến của đường tròn (O)
Tam giác ACO nội tiếp trong đường tròn (I) có OA là đường kính nên: ∠ ACO = 90 °
Suy ra: AC ⊥ OC tại C nên AC là tiếp tuyến của đường tròn (O)
* Biện luận
Luôn dựng được đường tròn tâm I, cắt đường tròn tâm O tại hai điểm B và C và luôn có AB, AC là hai tiếp tuyến của đường tròn (O).
GH
1 tháng 8 2023
a
Theo giả thiết có:
`AB=AC`
`OB=OC`
=> AO là đường trung trực của đoạn BC
=> AO⊥BC
b
Ta có:
`OB=OC=R`
Gọi điểm giao nhau của BC và OA là H có:
`HB=HC`
Từ trên suy ra: HO là đường trung bình của ΔCDB
=> HO//BD
=> OA//BD (H nằm trên đoạn OA)
GH
1 tháng 8 2023
c
AB là tiếp tuyến đường tròn.
=> OB⊥AB
Lại có: BH⊥OA (cmt)
Áp dụng hệ thức lượng vào tam giác OAB vuông tại B, đường cao BH có:
\(\dfrac{1}{BH^2}=\dfrac{1}{AB^2}+\dfrac{1}{OB^2}\\ \Leftrightarrow\dfrac{1}{BH^2}=\dfrac{1}{8^2}+\dfrac{1}{6^2}\\ \Rightarrow BH=\sqrt{1:\left(\dfrac{1}{8^2}+\dfrac{1}{6^2}\right)}=\dfrac{24}{5}=4,8\left(cm\right)\)
\(BC=2BH\left(BH=HC\right)\\ \Rightarrow BC=2.4,8=9,6\left(cm\right)\)
CM
11 tháng 11 2019
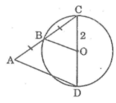
Trong tam giác ACD, ta có :
B là trung điểm của AC (gt)
O là trung điểm của CD
Nên OB là đường trung bình của ∆ACD
Suy ra : OB = (1/2).AD (tính chất đường trung bình của tam giác)
Vậy AD = 2.OB = 2.2 = 4 (cm)
24 tháng 6 2017
AB vuông góc OB tại B nên AB là tiếp tuyến của đường tròn (O). Tương tự, AC là tiếp tuyến của đường tròn (O)