Giúp mình bài 3 câu d với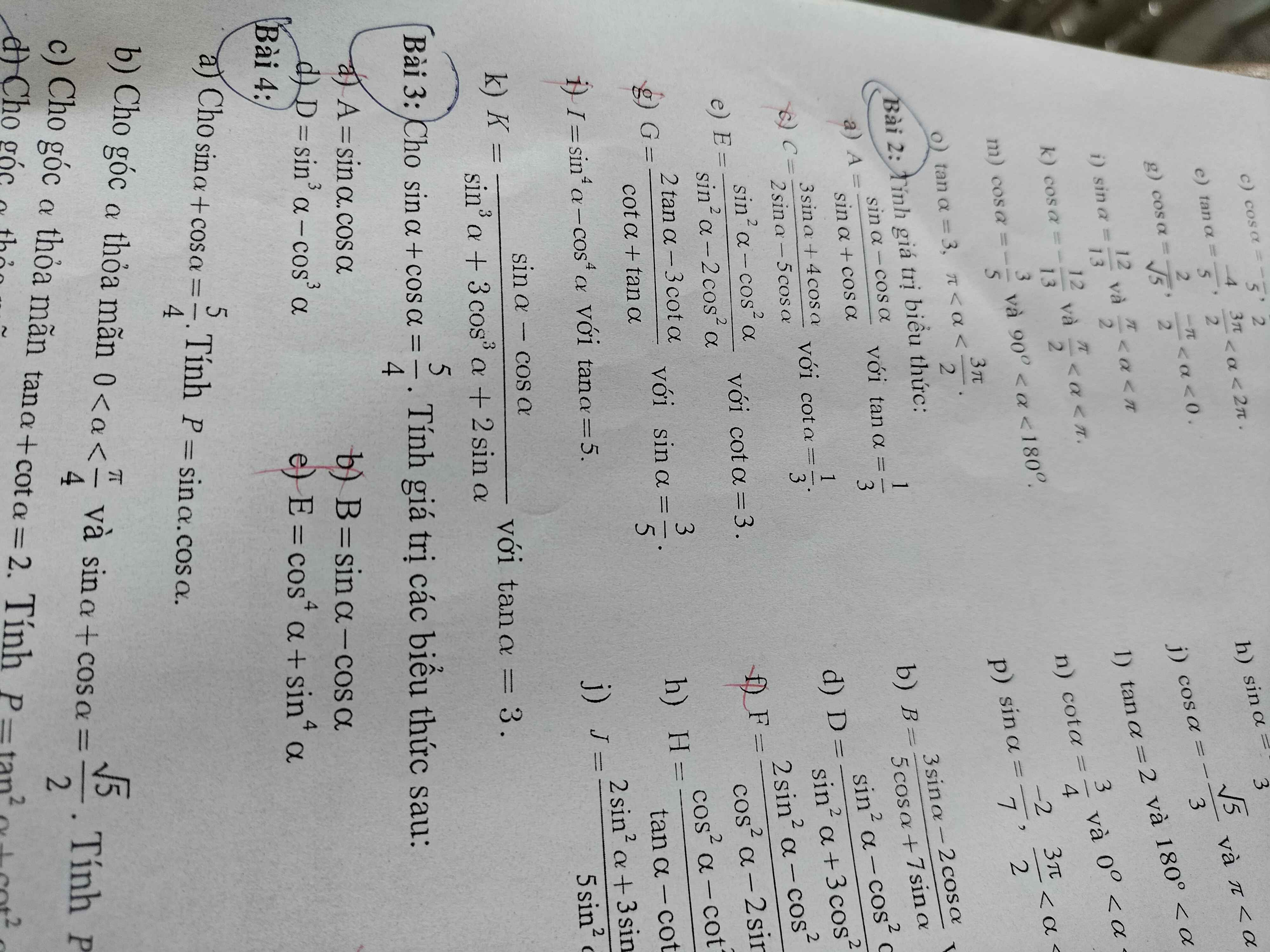
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(b,N=\left(2x-1\right)^2-4\ge-4\\ N_{min}=-4\Leftrightarrow x=\dfrac{1}{2}\\ c,P=\left(2x-5\right)^2+6\left(2x-5\right)+9-4\\ P=\left(2x-5+3\right)^2-4=\left(2x-2\right)^2-4\ge-4\\ P_{min}=-4\Leftrightarrow x=1\\ d,Q=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1\\ Q=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\\ Q_{min}=1\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
6a.
$M=x^2-x+1=(x^2-x+\frac{1}{4})+\frac{3}{4}$
$=(x-\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}$
Vậy $M_{\min}=\frac{3}{4}$ khi $x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}$

Bài 19:
a: \(A=5x+\dfrac{1}{9}y=5\cdot\dfrac{-1}{10}+\dfrac{1}{9}\cdot4.8=\dfrac{-1}{2}+\dfrac{8}{15}=\dfrac{-15+16}{30}=\dfrac{1}{30}\)
b: \(A=x-\dfrac{2}{3}=\dfrac{-1}{3}-\dfrac{2}{3}=-1\)
\(a,7x-2x-\dfrac{2}{3}y+\dfrac{7}{9}y=5x+\dfrac{1}{9}y\\ =5.\left(\dfrac{-1}{10}\right)+\dfrac{1}{9}.4,8\\ =\dfrac{-1}{2}+\dfrac{8}{15}=\dfrac{1}{30}\\ b,x=\dfrac{0,2-0,375+\dfrac{5}{11}}{-0,3+\dfrac{9}{16}-\dfrac{15}{22}}\\ =\dfrac{-1}{3}+\dfrac{\dfrac{-7}{40}+\dfrac{5}{11}}{\dfrac{21}{80}-\dfrac{15}{22}}\\ =\dfrac{-1}{3}+\dfrac{\dfrac{123}{440}}{\dfrac{-369}{880}}=\dfrac{-1}{3}+\dfrac{-2}{3}=\dfrac{-3}{3}=\left(-1\right)\)


12:
\(\dfrac{x}{y}\sqrt{\dfrac{y}{x}}=\dfrac{\sqrt{y}}{y}\cdot\dfrac{x}{\sqrt{x}}=\dfrac{\sqrt{x}}{\sqrt{y}}\)


2.1
\(\Leftrightarrow x^3+3x^2+2x-3x^2-9x-6=0\)
\(=x\left(x^2+3x+2\right)-3\left(x^2+3x+2\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x^2+3x+2\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x+1\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-1\\x=-2\end{matrix}\right.\)
2.2
\(\Leftrightarrow x^3-2x^2-2x-x^2+2x+2=0\)
\(\Leftrightarrow x\left(x^2-2x-2\right)-\left(x^2-2x-2\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2-2x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=1\pm\sqrt{3}\end{matrix}\right.\)
2.3
\(\Leftrightarrow3x^3-3x^2+2x+3x^2-3x+2=0\)
\(\Leftrightarrow x\left(3x^2-3x+2\right)+3x^2-3x+2=0\)
\(\Leftrightarrow\left(x+1\right)\left(3x^2-3x+2\right)=0\)
\(\Leftrightarrow x=-1\)
2.5
\(\Leftrightarrow2x^3+x^2+3x-4x^2-2x-6=0\)
\(\Leftrightarrow x\left(2x^2+x+3\right)-2\left(2x^2+x+3\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(2x^2+x+3\right)=0\)
\(\Leftrightarrow x=2\)

a) Gọi x, y lần lượt là số mol Al, Fe
2Al + 3H2SO4 → Al2(SO4)3 + 3H2
Fe + H2SO4 → FeSO4+ H2
\(\left\{{}\begin{matrix}27x+56y=5,54\\\dfrac{3}{2}x+y=\dfrac{3,584}{22,4}\end{matrix}\right.\)
=> x=0,06 , y =0,07
=> \(m_{Al}=1,62\left(g\right);m_{Fe}=3,92\left(g\right)\)
b) \(n_{H_2SO_4\left(pứ\right)}=n_{H_2}=0,16\left(mol\right)\)
=> \(m_{H_2SO_4\left(pứ\right)}=0,16.98=15,68\left(g\right)\)
c) \(m_{ddH_2SO_4}=\dfrac{15,68}{20\%}=78,4\left(g\right)\)
c) 2NaOH + H2SO4 → Na2SO4 + 2H2O
\(n_{H_2SO_4\left(dư\right)}=\dfrac{1}{2}n_{NaOH}=\dfrac{1}{2}.0,25.0,6=0,075\left(mol\right)\)
=> \(m_{H_2SO_4\left(bđ\right)}=15,68+0,075.98=23,03\left(g\right)\)


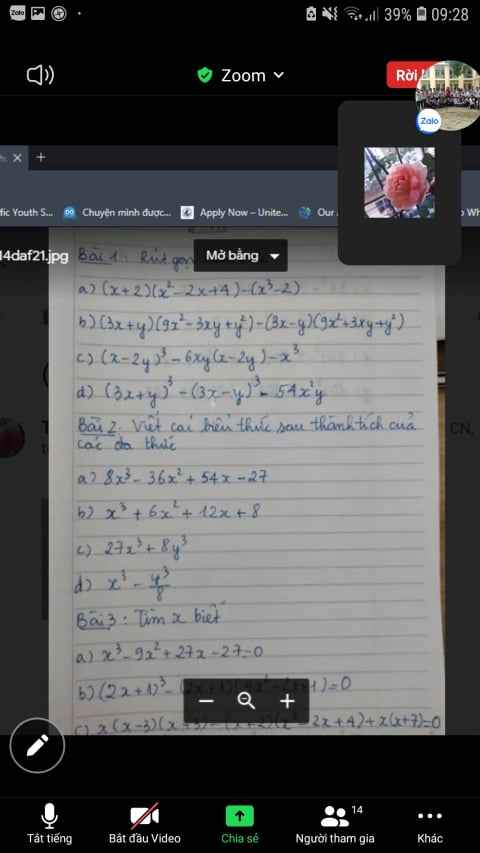

 bài 2 câu 1,2,3,5,9
bài 2 câu 1,2,3,5,9 



Lơ giải:
\(\frac{25}{16}=(\sin a+\cos a)^2=\sin ^2a+\cos ^2a+2\sin a\cos a=1+2\sin a\cos a\)
\(\Rightarrow \sin a\cos a=\frac{9}{32}\)
\((\sin a-\cos a)^2=(\sin a+\cos a)^2-4\sin a\cos a=\frac{25}{16}-4.\frac{9}{32}=\frac{7}{16}\)
\(\Rightarrow \sin a-\cos a=\pm \frac{\sqrt{7}}{4}\)
Do đó:
\(D=\sin ^3a-\cos ^3a=(\sin a-\cos a)(\sin ^2a+\sin a\cos a+\cos ^2a)\)
\(=(\sin a-\cos a)(1+\sin a\cos a)\)
\(=\pm \frac{\sqrt{7}}{4}(1+\frac{9}{32})=\pm \frac{41\sqrt{7}}{128}\)
Lơ giải:
\(\frac{25}{16}=(\sin a+\cos a)^2=\sin ^2a+\cos ^2a+2\sin a\cos a=1+2\sin a\cos a\)
\(\Rightarrow \sin a\cos a=\frac{9}{32}\)
\((\sin a-\cos a)^2=(\sin a+\cos a)^2-4\sin a\cos a=\frac{25}{16}-4.\frac{9}{32}=\frac{7}{16}\)
\(\Rightarrow \sin a-\cos a=\pm \frac{\sqrt{7}}{4}\)
Do đó:
\(D=\sin ^3a-\cos ^3a=(\sin a-\cos a)(\sin ^2a+\sin a\cos a+\cos ^2a)\)
\(=(\sin a-\cos a)(1+\sin a\cos a)\)
\(=\pm \frac{\sqrt{7}}{4}(1+\frac{9}{32})=\pm \frac{41\sqrt{7}}{128}\)