Một vật được thả rơi tự do từ độ cao 9 m so với mặt đất. Chọn gốc thế năng tại mặt đất. Lâý g = 10 m/s². Tính tốc độ của vật tại vị trí vật có động năng bằng một nửa thế năng.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2
28 tháng 5 2022
`@W_t=mgz=2.10.2=40(J)`
`W_đ=1/2mv^2=1/2 .2.0^2=0(J)`
`W=W_t+W_đ=40+0=40(J)`
`@W_[(W_đ=2W_t)]=W_[đ(W_đ=2W_t)]+W_[t(W_đ=2W_t)]=40`
Mà `W_[đ(W_đ=2W_t)]=2W_[t(W_đ=2W_t)]`
`=>3W_[t(W_đ=2W_t)]=40`
`<=>3mgz_[(W_đ=2W_t)]=40`
`<=>3.2.10.z_[(W_đ=2W_t)]=40`
`<=>z_[(W_đ=2W_t)]~~0,67(m)`
`@W_[đ(max)]=W_[t(max)]=40`
`<=>1/2mv_[max] ^2=40`
`<=>1/2 .2v_[max] ^2=40`
`<=>v_[max]=2\sqrt{10}(m//s)`
28 tháng 5 2022
Sao lại 3 lần thế năng? Trong khi đó có 2? giải thích giúp em.
26 tháng 3 2022
\(W_đ=2W_t\Leftrightarrow W_t=\dfrac{1}{3}W_đ\)
Theo định luật bảo toàn cơ năng, ta có
\(mgh=\dfrac{1}{3}.\dfrac{mv^2}{2}\Leftrightarrow0,5.10.h=8,3\\ \Rightarrow h=1,6\left(m\right)\)
\(W_đ=\dfrac{2}{3}W\Leftrightarrow\dfrac{mv^2}{2}=\dfrac{2}{3}.8,3\\ \Leftrightarrow\dfrac{0,5.v^2}{2}=8,3\\ \Rightarrow v=4\sqrt{6}\left(m/s\right)\)
22 tháng 2 2023
a, ta có ΔW = A ⇔ Wsau - Wtrc = A
→Wsau = A + Wtrc = 1,5.10.25 + \(\dfrac{1}{2}\).1,5.0
→ \(\dfrac{1}{2}\)m.v\(^2\)= 375 → v = 10\(\sqrt{5}\)
b,
Wđ = Wt
⇔ W = Wđ + Wt = 2Wt
mà cơ năng của vật là :
W = Wt = 375
→2mgh = 375
→h = \(\dfrac{375}{2g.m}\) = 12,5m
c,
Wđ = 3Wt
W = Wđ + Wt = 4Wt
→375 = 4m.g.h → h = 6,25 (m)
ta có S = \(\dfrac{1}{2}\).a.t\(^2\)= 6,25 → t = \(\sqrt{\dfrac{6,25.2}{10}}\)= \(\dfrac{\sqrt{5}}{2}\) (s)
N
30 tháng 3 2023
a. Thế năng của vật tại vị trí thả:
\(W_t=mgh=0,1\cdot10\cdot45=45\left(J\right)\)
Cơ năng của vật:
\(W=W_t+W_d=45+\dfrac{1}{2}\cdot 0,1\cdot0^2=45\left(J\right)\)
b. Ta có định luật bảo toàn cơ năng: \(W_A=W_B\)
\(\Leftrightarrow45=\dfrac{1}{2}\cdot0,1\cdot v_B^2+0\cdot10\cdot0,1\)
\(\Leftrightarrow v_B=30\left(\dfrac{m}{s}\right)\)
\(\Rightarrow W_{d_B}=\dfrac{1}{2}\cdot0,1\cdot30=45\left(J\right)\)
2
5 tháng 5 2022
`a)W_[t(60m)] = mgz_[60m] = 2 . 10 . 60 = 1200 (J)`
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
`b)W=W_[đ(max)] = W_[t(max)]`
`<=>1/2mv_[cđ]^2=mgz_[max]`
`<=>1/2 .2.v_[cđ]^2=2.10.80`
`<=>v_[cđ] = 40(m//s)`
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
`c)W=W_t+W_đ`
Mà `W_đ=3W_t`
`=>W=4W_t`
Hay `W = W_[t(max)]=mgz_[max]=2.10.80=1600(J)`
`=>1600=4W_t`
`=>400=mgz_[(W_đ = 3W_t)]`
`=>400=2.10.z_[(W_đ = 3W_t)]`
`=>z_[(W_đ=3W_t)]=20 (m)`
2
13 tháng 5 2022
`a)W_[t(max)]=mgz_[max]=0,1.10.10=10(J)`
`b)W_[t(5m)]=mgz_[5m]=0,1.10.5=5(J)`
ADBT cơ năng có: `W=W_[t(5m)]+W_[đ(5m)]=10`
`<=>mgz_[5m]+W_[đ(5m)]=10`
`<=>0,1.10.5+W_[đ(5m)]=10`
`<=>W_[đ(5m)]=5(J)`
`c)W=W_[đ(W_đ=3W_t)]+W_[t(W_đ=3W_t)]=10`
Mà `W_[đ(W_đ=3W_t)]=3W_[t(W_đ=3W_t)]`
`=>4W_[t(W_đ=3W_t)]=10`
`<=>4mgz_[(W_đ=3W_t)]=10`
`<=>4.0,1.10.z_[(W_đ=3W_t)]=10`
`<=>z_[(W_đ=3W_t)]=2,5(m)`
19 tháng 3 2022
Cơ năng ban đầu:
\(W=\dfrac{1}{2}mv^2+mgh=10m\cdot h\left(J\right)\)
Cơ năng tại nơi \(W_đ=5W_t\Rightarrow W_t=\dfrac{1}{5}W_đ\):
\(W'=\dfrac{1}{2}mv^2+mgz=\dfrac{1}{2}\cdot m\cdot5^2+\dfrac{1}{5}\cdot\dfrac{1}{2}\cdot m\cdot5^2=15m\left(J\right)\)
Bảo toàn cơ năng: \(W=W'\)
\(\Rightarrow10m\cdot h=15m\Rightarrow h=\dfrac{15}{10}=1,5m\)
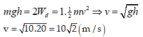
Cơ năng ban đầu:
\(W=mgz=m\cdot10\cdot9=90m\left(J\right)\)
Cơ năng tại nơi có \(W_đ=\dfrac{1}{2}W_t\Rightarrow W_t=2W_đ\):
\(W'=W_đ+W_t=3W_đ=3\cdot\dfrac{1}{2}mv^2\)
Bảo toàn cơ năng: \(W=W'\)
\(\Rightarrow90m=3\cdot\dfrac{1}{2}mv^2\Rightarrow v=2\sqrt{15}\)m/s