Cho tam giác ABC có AC=2BC và góc C= 2 góc A. CMR: tam giác ABC là tam giác vuông
2 người trả lời nhanh nhất mk sẽ tích đug nha
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
0
IM
14 tháng 11 2016
a)
Ta có :
\(\widehat{DAC}=\widehat{EAB}\left(=90^0+\widehat{BAC}\right)\)
=> \(\Delta DAC=\Delta EAB\left(c.g.c\right)\)
=> DC = EB ( hai cạnh tương ứng )
b)
Gọi giao điểm của DC với BE ; BA lần lượt là H và I
Vì \(\Delta DAC=\Delta EAB\)(c/m câu a)
=> \(\widehat{DAI}=\widehat{IBH}\)
Mà \(\widehat{DIA}=\widehat{HIB}\)( đối đnhr )
=> \(\widehat{DAI}=\widehat{IHB}=90^0\)
14 tháng 11 2016
a) Xét \(\Delta ADC,\Delta ABE\) có:
AD = AB ( gt )
\(\widehat{DAC}=\widehat{EAB}\left(=90^o+\widehat{BAC}\right)\)
AE = AC ( gt )
\(\Rightarrow\Delta DAC=\Delta EAB\left(c-g-c\right)\)
\(\Rightarrow DC=BE\) ( 2 cạnh tương ứng ) ( đpcm )
b) Gọi giao điểm giữa DC và AB là K
giao điểm giữa DC và BE là M
Ta có: \(\widehat{ADK}+\widehat{K_1}=90^o\) ( do \(\Delta DAK\) có \(\widehat{DAK}=90^o\) ) (1)
Vì \(\Delta ADC=ABE\)
\(\Rightarrow\widehat{ADC}=\widehat{ABE}\) ( 2 góc tương ứng )
hay \(\widehat{ADK}=\widehat{KBE}\) (2)
Mà \(\widehat{K_1}=\widehat{K_2}\) ( đối đỉnh ) (3)
Xét (1), (2) và (3) ta có:
\(\widehat{ADK}+\widehat{K_1}=90^o\)
Mà \(\widehat{ADK}=\widehat{KBE}\)
\(\widehat{K_1}=\widehat{K_2}\)
\(\Rightarrow\widehat{KBE}+\widehat{K_2}=90^o\)
Xét \(\Delta KBM\) có \(\widehat{KBE}+\widehat{K_2}=90^o\Rightarrow\widehat{KMB}=90^o\)
\(\Rightarrow BE\perp DC\left(đpcm\right)\)
7 tháng 2 2023
#\(N\)
`a,` Xét Tam giác `AMB` và Tam giác `AMC` có:
`AM` chung
`AB = AC (g``t)`
\(\widehat{AMB}=\widehat{AMC}=90^0\)
`=>` Tam giác `AMB =` Tam giác `AMC (ch-cgv)`
`b,` Vì Tam giác `AMB = ` Tam giác `AMC (a)`
`=>` \(\widehat{B}=\widehat{C}\) `(2` góc tương ứng `)`
`=>` \(\widehat{BAM}=\widehat{CAM}\) `( 2` góc tương ứng `)`
`=> AM` là tia phân giác của \(\widehat{BAC}\)
`c,` Xét Tam giác `AHM` và Tam giác `AKM` có:
`AM` chung
\(\widehat{HAM}=\widehat{KAM}(CMT)\)
`=>` Tam giác `AHM =` Tam giác `AKM (ch-gn)`
`=> AH = AK (2` cạnh tương ứng `)`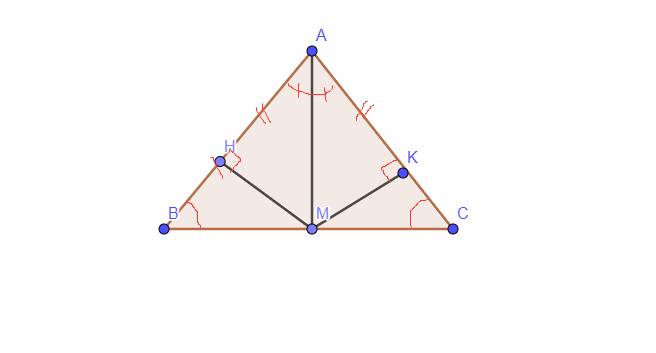
Gọi CF là phân giác của góc C=> gACF=gBCF.
Ta lại có gBAC=1/2 gACB => g.BAC =g.ACF (=1/2g.ACB)=> Tam giác AFC cân tại F.
Vẽ FE vuông góc với AC(E thuộc AC). Tam giác AFC cân tại F => EA=EC=1/2AC mà AC=2BC => EC=BC.
Xét tam giác BCF và tam giác ECF, ta có:
EC=BC
g.ECF =g.BCF(CF là phân giác của g.ACB)
FC chung
Do đó: tgBCF =tgECF(c.g.c) => g.ABC=g.CEF=90o
Vậy tam giác ABC vuông tại B.
thanks pạn nha