nguyên liệu làm nón lá bằng giấy
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
30 tháng 11 2019
Đáp án C
Gọi số chiếc nón lá mỗi ngày cơ sở đó làm được là x (chiếc)
Số ngày cơ sở đó dự kiến làm hết 300 chiếc nón lá là: 300/x (ngày)
Sau khi làm tăng thêm 5 chiếc nón lá một ngày thì thời gian cơ sở đó làm hết 300 chiếc nón lá là: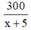 
(ngày).
Theo đề bài ta có phương trình:
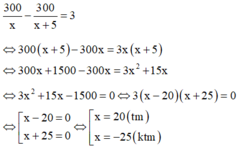
Vậy theo dự kiến, mỗi ngày cơ sở đó làm được 20 chiếc nón lá.
23 tháng 5 2022
Diện tích lá cần dùng cho một chiếc nón:
\(2(3,14.rl)=2(3,14.35.\dfrac{50}{2})=5495 (cm^2)\)
Vậy diện tích lá cần dùng cho một chiếc nón là \(5495 cm^2\)
CM
7 tháng 10 2019
Đáp án C
Diện tích của lá để làm cái nón lá chính là diện tích xung quanh của hình nón
Ta có S x q = πrl = π 5 2 . 5 = 25 π 2
22 tháng 6 2021
Bán kính nón là: 50 :2 =25 (cm)
Chiều cao của nón là: \(\sqrt{l^2-r^2}=\) \(\sqrt{35^2-25^2}=10\sqrt{6}\left(cm\right)\)
Thể tích của chiếc nón là: \(\dfrac{1}{3}\pi r^2h=\dfrac{1}{3}.\pi.25^2.10\sqrt{6}=16031,8\left(cm^3\right)\)
Diện tích phần là làm thân nón là: \(\pi rl=\pi.25.35=875\pi\left(cm^2\right)\)
CM
21 tháng 8 2018
Đáp án C
Ta có x = k . R là chu vi đường tròn đáy của khối nón ⇒ k . R = 2 π r ⇒ r = k . R 2 π
Độ dài đường sinh của khối nón chính là bán kính R ⇒ l = R = r 2 + h 2 ⇒ h = R 2 − r 2
Thể tích của khối nón là:
V = 1 3 π r 2 h = 1 3 π . r 2 . R 2 − r 2 ⇔ V 2 = π 2 9 . r 4 . R 2 − r 2 . 1
Theo bất đẳng thức Cosi, ta được r 2 . R 2 − r 2 = 4. r 2 2 . r 2 2 . R 2 − r 2 ≤ 4 R 6 27 2
Từ (1), (2) suy ra:
V = π 2 9 . 4 R 6 27 = 4 π 2 243 R 6 ⇒ V ≤ 2 π 9 3 R 3
Dấu “=” xảy ra khi:
⇔ r 2 2 = R 2 − r 2 ⇔ R 2 = 3 2 r 2 = 3 2 . k 2 R 2 4 π 2 ⇒ k 2 = 8 π 2 3 ⇒ k ≃ 5 , 13
ờm
bít ko