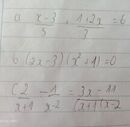
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 3:
a) Ta có: \(\left(x+10\right)^2+\left(x-10\right)^2\)
\(=x^2+20x+100+x^2-20x+100\)
\(=2x^2+200\)
b) Ta có: \(\left(x-12\right)^2+\left(x+12\right)^2\)
\(=x^2-24x+144+x^2+24x+144\)
\(=2x^2+288\)
c) Ta có: \(\left(x+7\right)^2-\left(x-7\right)^2\)
\(=\left(x+7-x+7\right)\left(x+7+x-7\right)\)
\(=14\cdot2x\)
=28x
Bài 1:
a) Ta có: \(\left(a+12\right)^2\)
\(=a^2+2\cdot a\cdot12+12^2\)
\(=a^2+24a+144\)
b) Ta có: \(\left(3a+\dfrac{1}{3}\right)^2\)
\(=\left(3a\right)^2+2\cdot3a\cdot\dfrac{1}{3}+\left(\dfrac{1}{3}\right)^2\)
\(=9a^2+2a+\dfrac{1}{9}\)
c) Ta có: \(\left(5a^2+6\right)^2\)
\(=\left(5a^2\right)^2+2\cdot5a^2\cdot6+6^2\)
\(=25a^4+60a^2+36\)
d) Ta có: \(\left(\dfrac{1}{2}+4b\right)^2\)
\(=\left(\dfrac{1}{2}\right)^2+2\cdot\dfrac{1}{2}\cdot4b+\left(4b\right)^2\)
\(=\dfrac{1}{4}+4b+16b^2\)
e) Ta có: \(\left(a^m+b^n\right)^2\)
\(=\left(a^m\right)^2+2\cdot a^m\cdot b^n+\left(b^n\right)^2\)
\(=a^{2m}+2a^mb^n+b^{2n}\)


x và y tỉ lệ thuận
nên \(\dfrac{x_1}{y_1}=\dfrac{x_2}{y_2}\)
Áp dụng tính chất của DTSBN, ta được:
\(\dfrac{x_1}{y_1}=\dfrac{x_2}{y_2}=\dfrac{2x_1-3x_2}{2y_1-3y_2}=\dfrac{42.5}{-8.5}=-5\)
=>x=-5y


các anh chiến sĩ thật gan dạ, quả cảm và đầy tình yêu thương.
1 từ: dũng cảm
1 câu: Những anh bộ đội trong bức ảnh đã không ngại gian khổ, dũng cảm vào dòng nước lũ để giúp đỡ người dân.


\(3,\)
Vì đa thức có nghiệm là \(\dfrac{1}{2}\) nên \(P\left(\dfrac{1}{2}\right)=\dfrac{1}{4}a+\dfrac{5}{2}-3=0\)
\(\Leftrightarrow\dfrac{1}{4}a=\dfrac{1}{2}\Leftrightarrow a=2\)
\(4,\)
\(a,P\left(x\right)=3-2x=0\Leftrightarrow x=\dfrac{3}{2}\)
\(b,Q\left(x\right)=x^2+2\ge2>0\)
Vậy \(Q\left(x\right)\) luôn dương hay \(Q\left(x\right)\) vô nghiệm

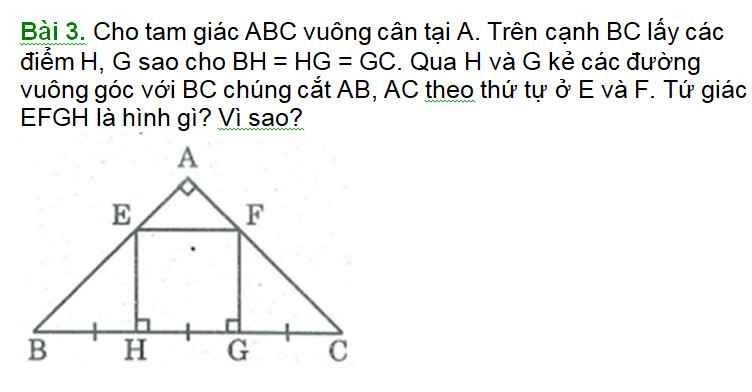
Xét tứ giác EHGF có:
EH//GF(cùng vuôn góc BC)
\(\widehat{EHG}=90^0\)(EH⊥HG)
=> EHGF là hình chữ nhật(1)
Xét tam giác EBG có:
EH là đường cao(EH⊥BG)
EH là trung tuyến(BH=HG)
=> Tam giác EBG cân tại E
Mà \(\widehat{EBH}=45^0\)(ABC vuông cân tại A)
=> Tam giác EBG vuông cân tại E
=> \(EH=\dfrac{1}{2}BG=HG\left(2\right)\)(EH là trung tuyến ứng với cạnh huyền)
\(\left(1\right),\left(2\right)\Rightarrow\) EHGF là hình vuông

\(21,B\\ 22,B\\ 23,C\\ 24,A\\ 25,B\\ 16,C\\ 17,C\\ 18,D\\ 19,B\\ 20,A\)
Hóa bạn qua bên box Hóa đăng nhé






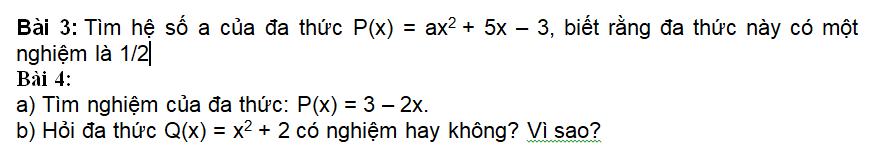




a) \(\frac{x-3}{5}+\frac{1+2x}{3}=6\)
<=> \(\frac{1}{5}x-\frac{3}{5}+\frac{1}{3}+\frac{2}{3}x=6\)
<=> \(\frac{13}{15}x=\frac{94}{15}\)<=> \(x=\frac{94}{13}\)
Vậy pt có nghiệm x = 94/13
b) ( 2x - 3 )( x2 + 1 ) = 0 (1)
Vì x2 + 1 ≥ 1 > 0 ∀ x
nên (1) <=> 2x - 3 = 0 <=> x = 3/2
Vậy pt có nghiệm x = 3/2
c) \(\frac{2}{x+1}-\frac{1}{x-2}=\frac{3x-11}{\left(x+1\right)\left(x-2\right)}\left(ĐKXĐ:\hept{\begin{cases}x\ne-1\\x\ne2\end{cases}}\right)\)
<=> \(\frac{2\left(x-2\right)}{\left(x+1\right)\left(x-2\right)}-\frac{x+1}{\left(x+1\right)\left(x-2\right)}=\frac{3x-11}{\left(x+1\right)\left(x-2\right)}\)
=> 2x - 4 - x - 1 = 3x - 11
<=> -4x = -6 <=> x = 3/2 (tm)
Vậy pt có nghiệm x = 3/2
a)\(\frac{x-3}{5}+\frac{1+2x}{3}=6\Leftrightarrow6\left(x-3\right)+10\left(1+2x\right)=180\)
\(\Leftrightarrow6x-18+10+20x=180\)
\(\Leftrightarrow26x-8=180\)
\(\Leftrightarrow26x=188\Rightarrow x=\frac{188}{26}=\frac{94}{13}\)
b)\(\left(2x-3\right)\left(x^2+1\right)=0\)
\(\orbr{\begin{cases}2x-3=0\\x^2+1=0\end{cases}\Rightarrow x=\frac{3}{2}}\)
c)\(\frac{2}{x+1}-\frac{1}{x-2}=\frac{3x-11}{\left(x+1\right)\left(x-2\right)}\)
\(\Leftrightarrow2\left(x-2\right)-1\left(x+1\right)=3x-11\)
\(\Leftrightarrow2x-4-x-1=3x-11\)
\(\Leftrightarrow11-5=3x-x\)
\(\Leftrightarrow6=2x\Rightarrow x=3\)