Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(a,\) Các hình thang \(BDEC;BDIC;BIEC\)
\(b,DE//BC.nên.\widehat{B_1}=\widehat{I_1}\left(so.le.trong\right)\)
Mà \(\widehat{B_1}=\widehat{B_2}\left(t/c.phân.giác\right)\) nên \(\widehat{B_2}=\widehat{I_1}\Rightarrow\Delta DIB\) cân tại D
\(\Rightarrow DI=DB\left(1\right)\)
\(DE//BC.nên.\widehat{C_1}=\widehat{I_2}\left(so.le.trong\right)\)
Mà \(\widehat{C_1}=\widehat{C_2}\left(t/c.phân.giác\right)\) nên \(\widehat{C_2}=\widehat{I_2}\Rightarrow\Delta IEC\) cân tại E
\(\Rightarrow EI=EC\left(2\right)\\ \left(1\right)\left(2\right)\Rightarrow DI+IE=BD+EC\\ \Rightarrow DE=BD+CE\left(Đpcm\right)\)
b: Xét ΔDBI có
\(\widehat{DBI}=\widehat{DIB}\)
nên ΔDBI cân tại D
Xét ΔEIC có \(\widehat{EIC}=\widehat{ECI}\)
nên ΔEIC cân tại E
Ta có: DE=DI+IE
nên DE=DB+EC
Vậy: BDEC là hình thang có một cạnh đáy bằng tổng hai cạnh bên
Đường thẳng đi qua I song song với BC cắt AB tại D và AC tại E, ta có các hình thang sau: BDEC, BDIC, BIEC
DE // BC (theo cách vẽ)
⇒ ∠ I 1 = ∠ B 1 (hai góc so le trong)
Mà ∠ B 1 = ∠ B 2 (gt)
Suy ra: ∠ I 1 = ∠ B 2
Do đó: ∆ BDI cân tại D ⇒ DI = DB (1)
Ta có: ∠ I 2 = ∠ C 1 (so le trong)
∠ C 1 = ∠ C 2 (gt)
Suy ra: ∠ I 2 = ∠ C 2 do đó: ∆ CEI cân tại E
⇒ IE = EC (2)
DE = DI + IE (3)
Từ (1), (2), (3) suy ra: DE = BD + CE
b) Ta có: \(\widehat{DBI}=\widehat{IBC}\)(gt)
mà \(\widehat{DIB}=\widehat{IBC}\)(hai góc so le trong, DI//BC)
nên \(\widehat{DBI}=\widehat{DIB}\)
hay ΔDIB cân tại D
Ta có: \(\widehat{EIC}=\widehat{ICB}\)(hai góc so le trong, IE//BC)
mà \(\widehat{ECI}=\widehat{ICB}\)(gt)
nên \(\widehat{EIC}=\widehat{ECI}\)
hay ΔEIC cân tại E
a,
Do \(DE||BC\) (gt) \(\Rightarrow BDEC\) là hình thang
Do \(DE||BC\Rightarrow DI||BC\Rightarrow BDIC\) là hình thang
Do \(DE||BC\Rightarrow IE||BC\Rightarrow BIEC\) là hình thang
b.
Do \(DI||BC\Rightarrow\widehat{CBI}=\widehat{BID}\) (so le trong)
Mà \(\widehat{CBI}=\widehat{DBI}\) (do BI là phân giác góc B)
\(\Rightarrow\widehat{DBI}=\widehat{BID}\)
\(\Rightarrow\Delta BDI\) cân tại D
Tương tự ta có \(\widehat{ICB}=\widehat{CIE}\) (so le trong) và \(\widehat{ICB}=\widehat{ICE}\) (do IC là phân giác góc C)
\(\Rightarrow\widehat{CIE}=\widehat{ICE}\Rightarrow\Delta IEC\) cân tại E
c.
Từ câu b, do \(\Delta BDI\) cân \(\Rightarrow DB=DI\)
Do \(\Delta IEC\) cân \(\Rightarrow IE=CE\)
\(\Rightarrow BD+CE=DI+IE=DE\left(đpcm\right)\)
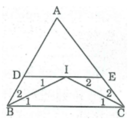
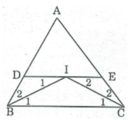
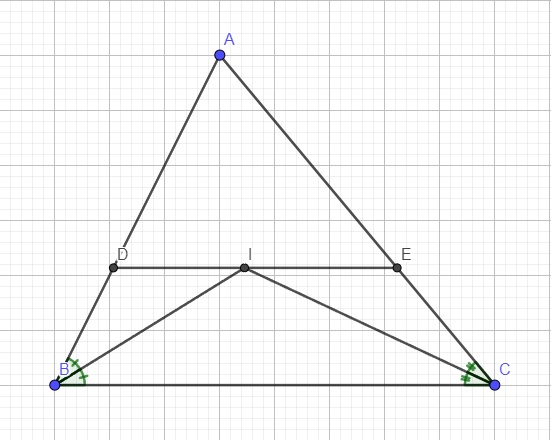
b) Ta có: DE//BC ( BDCE là hình thang )
=> DI, IE//BC
Ta có: DI//BC (cmt)
=> Góc CBI = góc DIB ( cặp góc so le trong )
Mà góc DBI = góc CBI ( BI là tia phân giác của góc B)
=> Góc DIB = góc DBI
=> DB = DI ( quan hệ giữa góc và cạnh đối diện) (1)
Ta có: IE//BC ( đã cm ở đầu bài)
=> Góc EIC = góc BCI ( cặp góc so le trong)
Mà góc ECI = góc BCI (CI là tia phân giác của góc C)
=> Góc EIC = góc ECI
=> EI = EC ( quan hệ giữa góc và cạnh đối diện) (2)
Từ (1) và (2) => DE = DB + EC
=> Đáy DE trong hình thang BDEC bằng tổng 2 cạnh bên.