Câu 1:
Cho tam giác ABC có AB=AC>BC
Gọi M,N lần lượt là trung điểm của AC,AB
Lấy điểm D sao cho M là trung điểm của ND
Tia AD cắt BC kéo dài tại E
a) Chứng minh tam giác AMN = tam giác CMD và AB//CD
b) Chứng minh tam giác NCB = tam giác CND và DN//BE
c) Chứng minh BCMN là hình thang cân và ANCE là hình thang
d) So sánh BD và NE

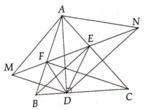


a) Xét tam giác AMN và tam giác CMD có:
MN = MD ( M là trung điểm của ND)
Góc NMA = góc DMC ( đối đỉnh)
MA = MC ( M là trung điểm của AC )
=> tam giác AMN = tam giác CMD ( c-g-c)
=> Góc NAM = góc DCM ( 2 góc tương ứng )
Mà 2 góc này ở vị trí so le trong => AN//DC=> AB//DC ( vì A, N, B là 3 điểm tạo nên cùng 1 đường thẳng).
b) Ta có: AN = DC ( tam giác AMN = tam giác CMD)
Mà AN = NB ( N là trung điểm của AB)
=> DC = NB
Xét tam giác NCB và tam giác CND có:
NC là cạnh chung
Góc BNC = góc DCN( so le trong, NB//DC)
NB = DC (cmt)
=> tam giác NCB = tam giác CND ( c-g-c)
=> Góc BCN = góc DNC ( 2 góc tương ứng)
Mà 2 góc này ở vị trí so le trong => ND//BC=> ND//BE
c) Ta có: ND//BE(cmt)=> NM//BC=> BCMN là hình thang (1)
Ta có: AB = AC (gt)
=> Góc ABC = góc ACB ( quan hệ giữa góc và cạnh đối diện)
=> Góc NBC = góc MCB (2)
Từ (1) và (2) => BCMN là hình thang cân
Xét tam giác AMD và tam giác CMN có:
MA = MC ( M là trung điểm của cạnh AC)
Góc DMA = góc NMC ( đối đỉnh)
MN = MD ( M là trung điểm của cạnh ND)
=> Tam giác AMD = tam giác CMN (c-g-c)
=> Góc DAM = góc NCM ( 2 góc tương ứng)
Mà 2 góc này ở vị trí so le trong => AE//NC => ANCE là hình thang
d) BD>NE