Tính : \(\dfrac{1}{1+\sqrt{2}}+\dfrac{1}{2+\sqrt{3}}+...+\dfrac{1}{20+\sqrt{21}}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 7 2023
1:
\(A=\sqrt{2-\sqrt{3}}\cdot\sqrt{2+\sqrt{2-\sqrt{3}}}\cdot\sqrt{2^2-\left(2+\sqrt{2-\sqrt{3}}\right)}\)
\(=\sqrt{2-\sqrt{3}}\cdot\sqrt{2+\sqrt{2-\sqrt{3}}}\cdot\sqrt{2-\sqrt{2-\sqrt{3}}}\)
\(=\sqrt{2-\sqrt{3}}\cdot\sqrt{4-2+\sqrt{3}}\)
\(=\sqrt{2-\sqrt{3}}\cdot\sqrt{2+\sqrt{3}}=1\)
MQ
1
14 tháng 7 2017
\(A=\dfrac{1}{1+\sqrt{2}}+\dfrac{1}{\sqrt{2}+\sqrt{3}}+...+\dfrac{1}{\sqrt{20}+\sqrt{21}}\)
\(=\sqrt{2}-1+\sqrt{3}-\sqrt{2}+....+\sqrt{21}-\sqrt{20}\)
\(=1-\sqrt{21}=\sqrt{21}-1\)
H9
HT.Phong (9A5)
CTVHS
8 tháng 9 2023
\(B=\left(\dfrac{4}{1-\sqrt{5}}+\dfrac{1}{2+\sqrt{5}}-\dfrac{4}{3-\sqrt{5}}\right)\left(\sqrt{5}-6\right)\)
\(B=\left[\dfrac{4\left(1+\sqrt{5}\right)}{\left(1-\sqrt{5}\right)\left(1+\sqrt{5}\right)}+\dfrac{2-\sqrt{5}}{\left(2+\sqrt{5}\right)\left(2-\sqrt{5}\right)}-\dfrac{4\left(3+\sqrt{5}\right)}{\left(3-\sqrt{5}\right)\left(3+\sqrt{5}\right)}\right]\left(\sqrt{5}-6\right)\)
\(B=\left[\dfrac{4\left(1+\sqrt{5}\right)}{1-5}+\dfrac{2-\sqrt{5}}{4-5}-\dfrac{4\left(3+\sqrt{5}\right)}{9-5}\right]\left(\sqrt{5}-6\right)\)
\(B=\left[-\dfrac{4\left(1+\sqrt{5}\right)}{4}-\dfrac{2-\sqrt{5}}{1}-\dfrac{4\left(3+\sqrt{5}\right)}{4}\right]\left(\sqrt{5}-6\right)\)
\(B=\left(-1-\sqrt{5}-2+\sqrt{5}-3-\sqrt{5}\right)\left(\sqrt{5}-6\right)\)
\(B=\left(-\sqrt{5}-6\right)\left(\sqrt{5}-6\right)\)
\(B=-\left(\sqrt{5}+6\right)\left(\sqrt{5}-6\right)\)
\(B=-\left(5-36\right)\)
\(B=-\left(-31\right)\)
\(B=31\)
_____________________________
\(\sqrt{48}-\dfrac{\sqrt{21}-\sqrt{15}}{\sqrt{7}-\sqrt{5}}+\dfrac{2}{\sqrt{3}+1}\)
\(=4\sqrt{3}-\dfrac{\sqrt{3}\left(\sqrt{7}-\sqrt{5}\right)}{\sqrt{7}-\sqrt{5}}+\dfrac{2\left(\sqrt{3}-1\right)}{\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)}\)
\(=4\sqrt{3}-\sqrt{3}-\dfrac{2\left(\sqrt{3}-1\right)}{2}\)
\(=3\sqrt{3}-\sqrt{3}+1\)
\(=2\sqrt{3}+1\)
10 tháng 7 2021
a) Ta có: \(A=3\sqrt{20}-\sqrt{45}+2\sqrt{18}+\sqrt{72}\)
\(=6\sqrt{5}-3\sqrt{5}+6\sqrt{2}+6\sqrt{2}\)
\(=3\sqrt{5}+12\sqrt{2}\)
b) Ta có: \(B=\dfrac{12}{3-\sqrt{5}}-\dfrac{16}{\sqrt{5}+1}\)
\(=\dfrac{12\left(3+\sqrt{5}\right)}{4}-\dfrac{16\left(\sqrt{5}-1\right)}{4}\)
\(=3\left(3+\sqrt{5}\right)-4\left(\sqrt{5}-1\right)\)
\(=9+3\sqrt{5}-4\sqrt{5}+4\)
\(=13-\sqrt{5}\)
c) Ta có: \(C=10\sqrt{\dfrac{1}{5}}+\dfrac{1}{5}\sqrt{125}-2\sqrt{20}\)
\(=\dfrac{10}{\sqrt{5}}+\dfrac{1}{5}\cdot5\sqrt{5}-2\cdot2\sqrt{5}\)
\(=2\sqrt{5}+\sqrt{5}-4\sqrt{5}\)
\(=-\sqrt{5}\)
10 tháng 7 2021
e) Ta có: \(E=\sqrt{\left(\sqrt{3}+1\right)^2}-\sqrt{\left(\sqrt{3}-2\right)^2}\)
\(=\sqrt{3}+1-2+\sqrt{3}\)
\(=2\sqrt{3}-1\)
f) Ta có: \(F=\sqrt{6+2\sqrt{5}}-\sqrt{9-4\sqrt{5}}\)
\(=\sqrt{5}+1-\sqrt{5}+2\)
=3
10 tháng 7 2021
e) Ta có: \(E=\sqrt{\left(\sqrt{3}+1\right)^2}-\sqrt{\left(\sqrt{3}-2\right)^2}\)
\(=\sqrt{3}+1-2+\sqrt{3}\)
\(=2\sqrt{3}-1\)
f) Ta có: \(F=\sqrt{6+2\sqrt{5}}-\sqrt{9-4\sqrt{5}}\)
\(=\sqrt{5}+1-\sqrt{5}+2\)
=3
10 tháng 7 2021
a) Ta có: \(A=3\sqrt{20}-\sqrt{45}+2\sqrt{18}+\sqrt{72}\)
\(=6\sqrt{5}-3\sqrt{5}+6\sqrt{2}+6\sqrt{2}\)
\(=3\sqrt{5}+12\sqrt{2}\)
b) Ta có: \(B=\dfrac{12}{3-\sqrt{5}}-\dfrac{16}{\sqrt{5}+1}\)
\(=\dfrac{12\left(3+\sqrt{5}\right)}{4}-\dfrac{16\left(\sqrt{5}-1\right)}{4}\)
\(=3\left(3+\sqrt{5}\right)-4\left(\sqrt{5}-1\right)\)
\(=9+3\sqrt{5}-4\sqrt{5}+4\)
\(=13-\sqrt{5}\)
11 tháng 4 2023
1: ĐKXĐ: x>1/2
=>\(\dfrac{x}{\sqrt{2x-1}}+\dfrac{x}{\sqrt[4]{4x-3}}=2\)
x^2-2x+1>=0
=>x^2>=2x-1
=>\(\dfrac{x}{\sqrt{2x-1}}>=1\)
Dấu = xảy ra khi x=1
(x^2-2x+1)(x^2+2x+3)>=0
=>x^4-4x+3>=0
=>x^4>=4x-3
=>\(\dfrac{x}{\sqrt[4]{4x-3}}>=1\)
=>VT>=2
Dấu = xảy ra khi x=1
2: 4x-1=x+x+2x-1
5x-2=x+2x-1+2x-1
\(\left(\dfrac{1}{\sqrt{x}}+\dfrac{1}{\sqrt{x}}+\dfrac{1}{\sqrt{2x-1}}\right)\left(\sqrt{x}+\sqrt{x}+\sqrt{2x-1}\right)>=9\)
=>\(\dfrac{1}{\sqrt{x}}+\dfrac{1}{\sqrt{x}}+\dfrac{1}{\sqrt{2x-1}}>=\dfrac{9}{\sqrt{x}+\sqrt{x}+\sqrt{2x-1}}\)
\(\left(\sqrt{x}+\sqrt{x}+\sqrt{2x-1}\right)^2< =3\left(4x-1\right)\)
=>\(\sqrt{x}+\sqrt{x}+\sqrt{2x-1}< =\sqrt{3\left(4x-1\right)}\)
=>\(\dfrac{2}{\sqrt{x}}+\dfrac{1}{\sqrt{2x-1}}>=\dfrac{3\sqrt{3}}{\sqrt{4x-1}}\)
Tương tự, ta cũng có: \(\dfrac{1}{\sqrt{x}}+\dfrac{2}{\sqrt{2x-1}}>=\dfrac{3\sqrt{3}}{\sqrt{5x-2}}\)
=>\(\dfrac{1}{\sqrt{x}}+\dfrac{1}{\sqrt{2x-1}}>=\sqrt{3}\left(\dfrac{1}{\sqrt{4x-1}}+\dfrac{1}{\sqrt{5x-2}}\right)\)
Dấu = xảy ra khi x=1
5 tháng 7 2021
a) Ta có: \(A=\sqrt{20}-2\sqrt{45}+3\sqrt{18}+\sqrt{72}\)
\(=2\sqrt{5}-6\sqrt{5}+9\sqrt{2}+6\sqrt{2}\)
\(=-4\sqrt{5}+15\sqrt{2}\)
b) Ta có: \(B=4\sqrt{\left(\sqrt{3}-1\right)^2}+2\sqrt{12}+4\sqrt{\dfrac{1}{2}}\)
\(=4\left(\sqrt{3}-1\right)+2\cdot2\sqrt{3}+\dfrac{4}{\sqrt{2}}\)
\(=4\sqrt{3}-4+4\sqrt{3}+2\sqrt{2}\)
\(=8\sqrt{3}+2\sqrt{2}-4\)
c) Ta có: \(C=\left(3+\dfrac{3-\sqrt{3}}{\sqrt{3}-1}\right)\left(3-\dfrac{3+\sqrt{3}}{1+\sqrt{3}}\right)\)
\(=\left(3+\sqrt{3}\right)\left(3-\sqrt{3}\right)\)
=9-3
=6
d) Ta có: \(D=\dfrac{1}{2+\sqrt{3}}+\dfrac{1}{2-\sqrt{3}}\)
\(=2-\sqrt{3}+2+\sqrt{3}\)
=4
9 tháng 10 2021
\(2,\\ a,PT\Leftrightarrow\sqrt{\left(5x-1\right)^2}=\sqrt{4\left(x+1\right)^2}\\ \Leftrightarrow\left|5x-1\right|=2\left|x+1\right|\\ \Leftrightarrow\left[{}\begin{matrix}5x-1=2\left(x+1\right)\\1-5x=2\left(x+1\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}3x=3\\7x=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{1}{7}\end{matrix}\right.\)
\(b,ĐK:x^2-3\ge0\\ PT\Leftrightarrow\sqrt{x^2-3}=x-1\\ \Leftrightarrow x^2-3=x^2-2x+1\\ \Leftrightarrow2x=4\Leftrightarrow x=2\left(tm\right)\\ c,ĐK:x\le\dfrac{7}{2}\\ PT\Leftrightarrow7-2x=x^2+7\\ \Leftrightarrow x^2+2x=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\left(tm\right)\\x=2\left(tm\right)\end{matrix}\right.\\ d,ĐK:x\ge3\\ PT\Leftrightarrow3\sqrt{x-3}+\dfrac{1}{2}\cdot2\sqrt{x-3}-9\cdot\dfrac{1}{3}\sqrt{x-3}=2\\ \Leftrightarrow\sqrt{x-3}=2\\ \Leftrightarrow x-3=4\Leftrightarrow x=7\left(tm\right)\)
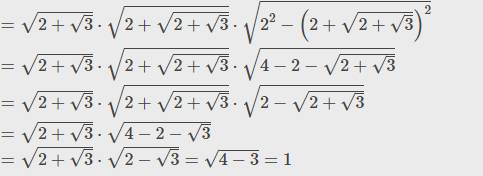
\(1=2-1=\left(\sqrt{2}-1\right)\left(\sqrt{2}+1\right)\)=>\(\dfrac{1}{1+\sqrt{2}=}=\dfrac{\left(\sqrt{2}-1\right)\left(\sqrt{2}+1\right)}{1+\sqrt{2}}=\sqrt{2}-1\)
cmtt thì biểu thức thành
\(\sqrt{2}-1+\sqrt{3}-\sqrt{2}+...+\sqrt{21}-\sqrt{20}\)=\(1+\sqrt{21}\)
bạn sửa giùm mình là \(\sqrt{21}-1\)