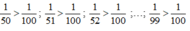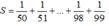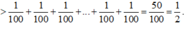CHỨNG MINH RẰNG 1/151+1/152+...+1/200>1/4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(\frac{1}{101}+\frac{1}{102}+...+\frac{1}{200}\)
\(=\left(\frac{1}{101}+\frac{1}{102}+...+\frac{1}{150}\right)+\left(\frac{1}{151}+\frac{1}{152}+...+\frac{1}{200}\right)>\frac{1}{150}\times50+\frac{1}{200}\times50\)
\(>\frac{1}{3}+\frac{1}{4}=\frac{7}{12}\)
b) \(\frac{1}{151}+\frac{1}{152}+...+\frac{1}{200}>\frac{1}{200}\times50=\frac{1}{4}\)
a)\(\frac{1}{101}+\frac{1}{102}+...+\frac{1}{200}\)
=\(\left(\frac{1}{101}+\frac{1}{102}+...+\frac{1}{150}\right)+\left(\frac{1}{151}+\frac{1}{152}+...+\frac{1}{200}\right)>\frac{1}{150}x50+\frac{1}{200}x50\)
\(>\frac{1}{3}+\frac{1}{4}=\frac{7}{12}\)
\(\frac{1}{151}+\frac{1}{152}+...+\frac{1}{200}>x50=\frac{1}{4}\)
Chúc bạn học tốt!

\(A=\frac{1}{151}+\frac{1}{152}+...+\frac{1}{200}>\frac{1}{200}+\frac{1}{200}+...+\frac{1}{200}=\frac{50}{200}=\frac{1}{4}\)
\(\Rightarrow A>\frac{1}{4}\)
đúng thì cho mik nha
\(A=\frac{1}{151}+\frac{1}{152}+...+\frac{1}{200}\) ( gồm 50 số hạng )
Ta thấy : \(\frac{1}{151}>\frac{1}{152}>...>\frac{1}{200}\)
\(\Rightarrow\frac{1}{151}+\frac{1}{152}+...+\frac{1}{200}>\frac{1}{200}+\frac{1}{200}+...+\frac{1}{200}\) ( gồm 50 số hạng \(\frac{1}{200}\))
\(\Rightarrow\frac{1}{151}+\frac{1}{152}+...+\frac{1}{200}>\frac{1}{200}.50\)
\(\Rightarrow\frac{1}{151}+\frac{1}{152}+...+\frac{1}{200}>\frac{50}{200}\)
\(\Rightarrow\frac{1}{151}+\frac{1}{152}+...+\frac{1}{200}>\frac{1}{4}\)
Hay \(A>\frac{1}{4}\)
Vậy \(A>\frac{1}{4}\)
_HT_

\(A=\frac{1}{151}+\frac{1}{152}+...+\frac{1}{200}\) ( Gồm 50 số hạng )
Ta thấy \(\frac{1}{151}>\frac{1}{152}>...>\frac{1}{200}\)
\(\Rightarrow\frac{1}{151}+\frac{1}{152}+...+\frac{1}{200}>\frac{1}{200}\times50\)
\(\Rightarrow\frac{1}{151}+\frac{1}{152}+...+\frac{1}{200}>\frac{50}{200}=\frac{1}{4}\)
\(\Rightarrow A>\frac{1}{4}\)
Vậy \(A>\frac{1}{4}\)
_HT_

(1+1/2+1/3+1/4)+(1/5+1/6+...+1/199+1/200)
=25/12+ biểu thức trong ngoặc
Vậy => đpcm

`Answer:`
Tổng: `(200-100):1+1=100` số hạng
Ta có:
\(\frac{1}{101}>\frac{1}{200}\)
\(\frac{1}{102}>\frac{1}{200}\)
...
\(\frac{1}{200}=\frac{1}{200}\)
\(\Rightarrow A>\frac{1}{200}+\frac{1}{200}+...+\frac{1}{200}\)
\(\Rightarrow A>\frac{100}{200}\)
\(\Rightarrow A>\frac{1}{2}\)