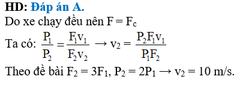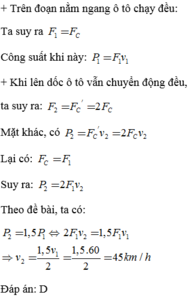Một xe đầu kéo lúc đầu chạy đều không tải trên đường nằm ngang với vận tốc 80 km/h, khi kéo thêm rơ-moóc, lực cản tăng gấp 2,5 lần nên tài xế tăng ga hết cỡ thì công suất động cơ lên gấp 2 lần so với lúc đầu. Tính vận tốc tối đa của xe khi kéo rơ-moóc. ĐS: 64 km/h.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(54\left(\dfrac{km}{h}\right)=15\left(\dfrac{m}{s}\right)\\ 13,5km=13500m\)
Công thực hiện là
\(A=F.s=2000.13500=27,000,000\left(J\right)\)
Công suất là
\(P=Fv=2000.15=30,000W\)
Công suất xe sau khi tăng 2 lần là
\(P_2=2P=60,000W\)
Công gây ra sau khi tăng 2 lầm công suất là
\(A=P.t=P.\dfrac{s}{v}=54,000,000J\)
Lực kéo lúc này là
\(F=\dfrac{A}{s}=\dfrac{54,000,000}{13500}=4000N\)
Tóm tắt
v=54km/h=15m/sv=54km/h=15m/s
s=13,5km=13500ms=13,5km=13500m
F=200NF=200N
a, A=? ; P=?
b, P′=2P⇒A′;F′=?
Giải
a, Công của động cơ là:
A=F.s=200.13500=2700000(J)=2700(kJ)
Công suất của động cơ là:
P=A/t=Fs/t=Fv=200.15=3000(W)
Thời gian đi hết quãng đường là:
t=s/v=13500/15=900(s
b,
+Khi tăng công suất lên 2 lần thì:
Công của động cơ là:
A′=2P.t=2.3000.900=5400000(J)=5400(kJ)
Lực kéo của động cơ là:
F′=A′/s=5400000/13500=400(N)

Tóm tắt:
\(s=18km\\ =18000m\\ t=30min\\ =1800s\\ F=2000N\\ ------------\\ A=?J\\ P\left(hoa\right)=?W\)
Động cơ xe tăng gấp 2 thì
\(v=?m/s\)
Giải:
Công: \(A=F.s\\ =2000.18000=36000000\left(J\right)\)
Công suất của xe: \(P\left(hoa\right)=\dfrac{A}{t}\\ =\dfrac{36000000}{1800}=20000\left(W\right)\)
Vận tốc của xe lúc này: \(v=\dfrac{s}{t}\\ =\dfrac{18000}{1800}=10\left(m/s\right)\)
Nếu động cơ xe tăng gấp 2 lần thì vận tốc xe là: \(10.2=20\left(m/s\right).\)

a. Ta có: \(\left\{{}\begin{matrix}s=v_0t+\dfrac{1}{2}at^2\Leftrightarrow24=v_0\cdot4+\dfrac{1}{2}\cdot a\cdot4^2\Leftrightarrow24=v_0\cdot4+8a_{\left(1\right)}\\v_0+at=0\Leftrightarrow v_0=-a\cdot4_{\left(2\right)}\end{matrix}\right.\)
Thay (2) vào (1): \(24=8a-16a\)
\(\Rightarrow a=-3\left(\dfrac{m}{s^2}\right)\)
\(\Rightarrow v_0=-at=-3\cdot-4=12\left(\dfrac{m}{s}\right)\)
b. \(F_{ham}=ma=2000\cdot-3=-6000\left(N\right)\)
c. \(F'_{ham}=3F_{ham}=3\cdot-6000=-18000\left(N\right)\)
\(F'_{ham}=ma'\Rightarrow a'=\dfrac{F'_{ham}}{m}=\dfrac{-18000}{2000}=-9\left(\dfrac{m}{s^2}\right)\)
\(v^2-v_0^2=2a'S'\)
\(\Leftrightarrow0^2-12^2=2\cdot-9\cdot S'\)
\(\Leftrightarrow-144=-18\cdot S'\)
\(\Rightarrow S'=8\left(m\right)\)