Một đa giác có số đường chéo nhiều hơn số cạnh là 18. Vậy số cạnh của đa giác đó là bao nhiêu cạnh.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 8 2021
a. Đa giác n đỉnh có \(C_n^2\) đoạn thẳng nối các đỉnh
Trong đó có n cạnh (là đường nối 2 đỉnh liền kế)
\(\Rightarrow\) Có \(C_n^2-n\) đường chéo
b. Cứ 3 đỉnh tạo thành 1 tam giác nên số tam giác là: \(C_n^3\)
c. Tam giác có 2 cạnh là 2 cạnh của tam giác khi 3 đỉnh của tam giác là 3 đỉnh liền kề
\(\Rightarrow\) có n tam giác thỏa mãn
d. Số tam giác chỉ có 1 cạnh là cạnh đa giác: có n cách chọn 2 điểm liền kề, ta có \(n-4\) cách chọn 1 điểm còn lại ko kề với 2 điểm trên
\(\Rightarrow n\left(n-4\right)\) tam giac thỏa mãn
e. Số tam giác thỏa mãn: \(C_n^3-\left(n+n\left(n-4\right)\right)\)
CM
15 tháng 11 2019
Số đường chéo của đa giác n cạnh là (n( n - 3 ))/2. ( n ∈ N, n ≥ 3 )
Theo giả thiết ta có (n( n - 3 ))/2 = n ⇔ n( n - 3 ) = 2n ⇔ n 2 - 3 n - 2 n = 0
⇔
n
2
-
5
n
=
0
⇔
n
(
n
-
5
)
=
0
⇔ 
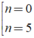
So sánh điều kiện ta có n = 5 thỏa mãn.
Chọn A
3 tháng 9 2021
Số đường chéo của đa giác đều n cạnh là \(\dfrac{n\left(n-3\right)}{2}\)
Số đường chéo bằng 33 số cạnh
\(\Rightarrow\dfrac{n\left(n-3\right)}{2}=33n\Rightarrow n\left(n-3\right)=66n\\
\Rightarrow n-3=66\\
\Rightarrow n=69\)
Suy ra đa giác đều đó có 69 cạnh
Số đo mỗi góc là \(\dfrac{180\cdot33+360}{69}\approx91,3\)
PT
1
B
0