cho tam giác ABC vuông cân tại A .Trên cạnh AB lấy điểm D ,trên tia đối của tia AC lấy điểm E sao cho AD=AE .CMR ED vuông với BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 7 2023
a: góc FEB+góc FBE=45+45=90 độ
=>EF vuông góc BC
b: ΔDFC vuông tại F có góc C=45 độ
nên ΔDFC vuông cân tại F
=>FD=FC
c: Xét ΔBEC có
EF,CA là đường cao
EF cắt CA tại D
=>D là trực tâm
=>BD vuông góc CE
21 tháng 9 2023
Tham khảo:
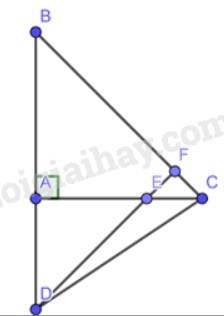
a) Vì tam giác ABC vuông cân tại A
\( \Rightarrow \) \(\widehat B = \widehat C = {45^o}\)(2 góc ở đáy bằng nhau)
Xét tam giác AED có :
AE = AD
AC vuông góc với AB
\( \Rightarrow \) Tam giác AED vuông cân tại A
\( \Rightarrow \widehat {ADE} = \widehat {AED} = {45^o}\)
Mà \(\widehat {AED};\widehat {CEF}\)là 2 góc đối đỉnh \( \Rightarrow \widehat {AED} = \widehat {CEF} = {45^o}\)
Xét tam giác CEF áp dụng định lí tổng 3 góc trong tam giác ta có :
\( \Rightarrow \widehat F + \widehat C + \widehat E = {180^o}\)
\( \Rightarrow \widehat F = {180^o} - {45^o} - {45^o} = {90^o} \Rightarrow EF \bot BC \Rightarrow DE \bot BC\)
b) Vì DE vuông góc với BC \( \Rightarrow \) DE là đường cao của tam giác BCD
Vì AC cắt DE tại E nên E là trực tâm tam giác BCD (Do AC cũng là đường cao của tam giác BCD)
\( \Rightarrow \)BE cùng là đường cao của tam giác BCD (định lí 3 đường cao trong tam giác đi qua trực tâm)
\( \Rightarrow \)BE vuông góc với DC
13 tháng 7 2023
a: Xét ΔABC vuông tại A và ΔADE vuông tại A có
AB=AD
AC=AE
=>ΔABC=ΔADE
b: góc DEB+góc CBA=45+45=90 độ
=>DE vuông góc BC tại H
c: Sửa đề: H là giao của DE với BC
Xét ΔHEB vuông tại H có góc HEB=45 độ
nên ΔHEB vuông cân tại H
=>HE=HB
30 tháng 9 2021
a: Xét ΔABC vuông tại A và ΔADE vuông tại A có
AB=AD
AC=AE
Do đó: ΔABC=ΔADE
Suy ra: BC=DE
1 tháng 10 2021
Bài 5: Cho tam giác ABC vuông tại A có AB < AC. Trên cạnh AC lấy điểm D sao cho AD = AB. Trên tia đối của tia AB lấy điểm E sao cho AE = AC. Chứng minh rằng: a) DE = BC b) DE vuông góc với BC
gọi K là giao của ED và BC
ΔAED vuông tại A có AD=AE
nên ΔAED vuông cân tại A
góc KCE+góc KEC=45+45=90 độ
=>ED vuông góc BC