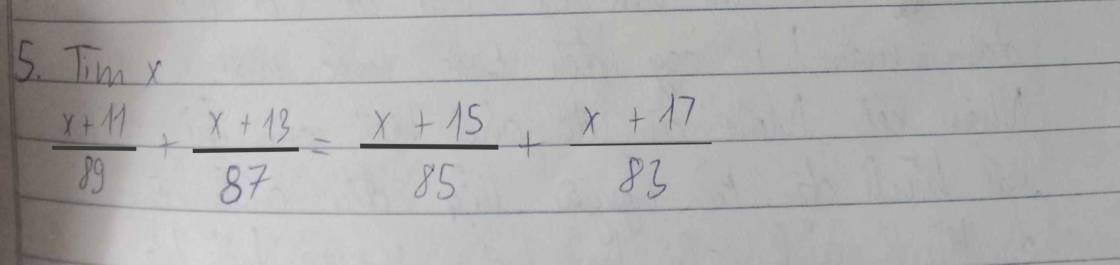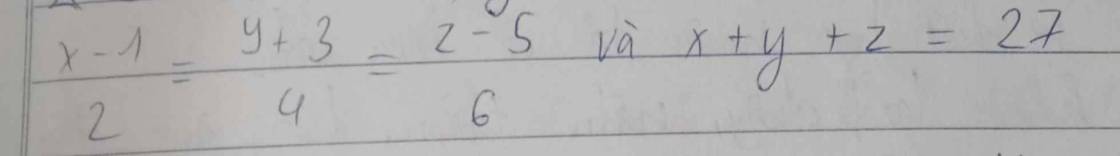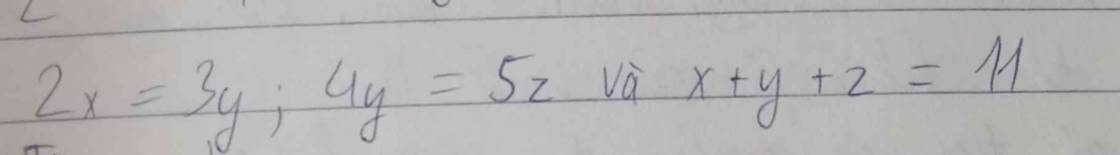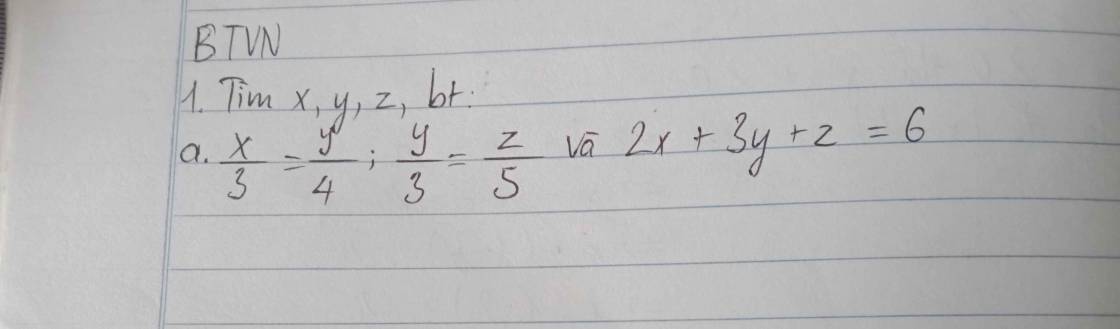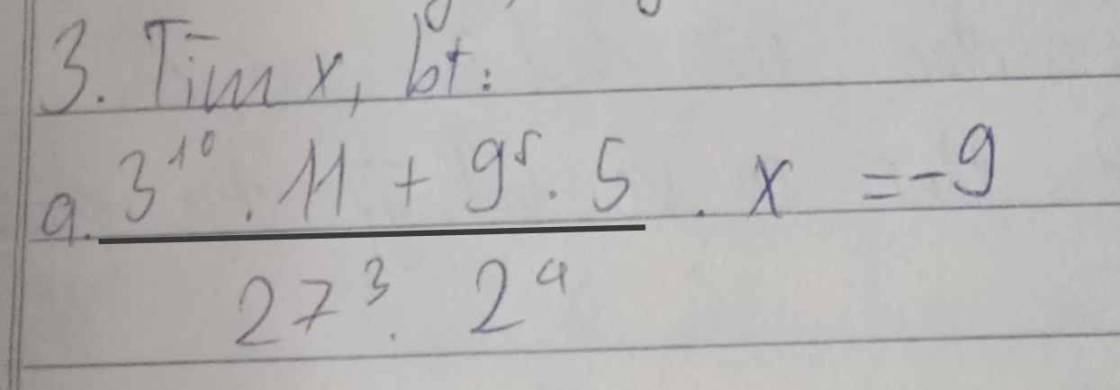giúp mình giải bài tập 2 với ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
SN
1 tháng 3 2017
Bài 39
Gọi x ( đồng ) là tiền mua loại hàng thứ nhất không kể VAT ( 0 < x < 110 000 )
Tiền mua loại hàng thứ nhất không kể VAT là 110 000 - x
Số tiền thực sự Lan đã trả cho loại hàng 1 : x + 0,1x
Số tiền thực sự Lan đã trả cho loại hàng 2 :
110 000 - x + 0,08 ( 110 000 - x )
Ta có phương trình
\(x+0,1x+110000-x+0,08\left(110000-x=120000\right)\)
=> 0,1x + 110 000 + 8800 - 0,08 x = 120000
=> 0,02 x = 1200
=> x = 6000
Vậy số tiền phải trả cho loại hàng thứ nhất là 6000
Số tiền phải trả cho loại hàng thứ 2 không kể VAT là 5000
Ủng hộ tk Đúng nhé bạn !
1 tháng 3 2017
nhiều bài 39 , 42 lắm đấy , bạn phải nói trang bn chứ
NH
1
NH
2
H
26 tháng 12 2022
Giải :
\(\dfrac{x+11}{89}+\dfrac{x+13}{87}-\dfrac{x+15}{85}-\dfrac{x+17}{83}=0\\ =>\left(\dfrac{x+11}{89}+1\right)+\left(\dfrac{x+13}{87}+1\right)-\left(\dfrac{x+15}{85}+1\right)-\left(\dfrac{x+17}{83}+1\right)=0\\ =>\left(\dfrac{x+11+89}{89}\right)+\dfrac{x+13+87}{87}-\dfrac{x+15+85}{85}-\dfrac{x+17+83}{83}=0\\ =>\dfrac{x+100}{89}+\dfrac{x+100}{87}-\dfrac{x+100}{85}-\dfrac{x+100}{83}=0\\ =>\left(x+100\right)\left(\dfrac{1}{89}+\dfrac{1}{87}-\dfrac{1}{85}-\dfrac{1}{83}\right)=0\\ =>\left[{}\begin{matrix}x+100=0\\\dfrac{1}{89}+\dfrac{1}{87}-\dfrac{1}{85}-\dfrac{1}{83}=0\left(voli\right)\end{matrix}\right.=>x=-100\)
NH
1
NH
2
H
26 tháng 12 2022
\(2x=3y\\ =>\dfrac{x}{3}=\dfrac{y}{2}\\ 4y=5z\\ =>\dfrac{y}{5}=\dfrac{z}{4}\\ \dfrac{x}{3}=\dfrac{y}{2}\\ =>\dfrac{x}{3.5}=\dfrac{y}{2.5}\\ =>\dfrac{x}{15}=\dfrac{y}{10}\\ \dfrac{y}{5}=\dfrac{z}{4}\\ =>\dfrac{y}{5.2}=\dfrac{z}{4.2}\\ =>\dfrac{y}{10}=\dfrac{z}{8}\\ =>\dfrac{x}{15}=\dfrac{y}{10}=\dfrac{z}{8}\)
Áp dụng tính chất dãy tỉ số bằng nhau
\(\dfrac{x}{15}=\dfrac{y}{10}=\dfrac{z}{8}=\dfrac{x+y+z}{15+10+8}=\dfrac{11}{33}=\dfrac{1}{3}\\ =>\left\{{}\begin{matrix}x=\dfrac{1}{3}.15=5\\y=\dfrac{1}{3}.10=\dfrac{10}{3}\\z=\dfrac{1}{3}.8=\dfrac{8}{3}\end{matrix}\right.\)
NH
2
H
26 tháng 12 2022
Giải
\(\dfrac{x}{3}=\dfrac{y}{4}\\ \Leftrightarrow\dfrac{x}{3.3}=\dfrac{y}{4.3}\\\Leftrightarrow\dfrac{x}{9}=\dfrac{y}{12}\\ \dfrac{y}{3}=\dfrac{z}{5}\\ \Leftrightarrow \dfrac{y}{3.4}=\dfrac{z}{5.4}\\ \Leftrightarrow\dfrac{y}{12}=\dfrac{z}{20}\\ =>\dfrac{x}{9}=\dfrac{y}{12}=\dfrac{z}{20}\)
Áp dụng tính chất dãy tỉ số bằng nhau
\(\dfrac{x}{9}=\dfrac{y}{12}=\dfrac{z}{20}=\dfrac{2x+3x+z}{2.9+3.12+20}=\dfrac{6}{74}=\dfrac{3}{37}\\ \Rightarrow\left\{{}\begin{matrix}x=\dfrac{3}{37}\times9=\dfrac{27}{37}\\y=\dfrac{3}{37}\times12=\dfrac{36}{37}\\z=\dfrac{3}{37}\times20=\dfrac{60}{37}\end{matrix}\right.\)
NH
2
NH
2
H
26 tháng 12 2022
\(a,\dfrac{3^{10}.11+9^5.5}{27^3.2^4}.x=-9\\ =>\dfrac{3^{10}.11+\left(3^2\right)^5.5}{\left(3^3\right)^3.2^4}.x=-9\\ =>\dfrac{3^{10}.\left(11+5\right)}{3^9.2^4}.x=-9\\ =>\dfrac{3^{10}.16}{3^9.2^4}.x=-9\\ =>\dfrac{3^{10}.2^4}{3^9.2^4}.x=-9\\ =>3^1.x=-9\\ =>x=-9:3\\ =>x=-3\)
