tìm x sao cho M dương của M=(x+3)(x+9)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 12 2021
a: \(M=\dfrac{x^2-3x+2x^2+6x-3x^2-9}{\left(x-3\right)\left(x+3\right)}=\dfrac{3}{x+3}\)
23 tháng 11 2019
a. \(m^3\)\(+n^3+m\)⋮\(mn\)⇔\(\left(m+n\right)^3+m\)\(-3mn\left(m+n\right)\)⋮\(mn\)
⇒ \(\left(m+n\right)^3+m\)⋮\(mn\)⇒\(\left(m+n\right)^3+m\)⋮\(m\)
⇒\(n\)⋮\(m\)
Đặt \(n=mk\)
Do \(\left(m+n\right)^3+m\)⋮\(m\)⇒\(\left(m+n\right)^3+m=pmn=pkm^2\)
⇒\(\left(m+n\right)^3=m\left(mnp-1\right)\)
Suy ra \(\left(mnp-1,m\right)=1\)⇒\(m=t^3\)
S
13 tháng 6 2021
Xét phương trình: \(x^2-2\left(m+3\right)x+2m+5=0\Rightarrow\Delta'=\left(m+3\right)^2-2m-5=\left(m+2\right)^2\ge0\) .
Do đó phương trình luôn có 2 nghiệm và để phương trình có 2 nghiệm phân biệt thì \(m\ne-2.\)
Theo định lý viet thì ta có: \(\hept{\begin{cases}x_1+x_2=2m+6\\x_1x_2=2m+5\end{cases}}\). Do đó: \(m>-\frac{5}{2}\)\(\frac{1}{\sqrt{x_1}}+\frac{1}{\sqrt{x_2}}=\frac{4}{3}\Rightarrow\frac{1}{x_1}+\frac{1}{x_2}+2\sqrt{\frac{1}{x_1x_2}}=\frac{x_1+x_2}{x_1x_2}+2\sqrt{\frac{1}{2m+5}}=\frac{16}{9}\)
\(\Leftrightarrow\frac{2m+6}{2m+5}+2\sqrt{\frac{1}{2m+5}}=\frac{1}{2m+5}+2\sqrt{\frac{1}{2m+5}}+1=\left(\sqrt{\frac{1}{2m+5}}+1\right)^2=\frac{16}{9}\)
\(\Rightarrow\sqrt{\frac{1}{2m+5}}=\frac{1}{3}\Leftrightarrow\frac{1}{2m+5}=\frac{1}{9}\Leftrightarrow2m+5=9\Leftrightarrow m=2.\)
Vậy \(m=2.\)
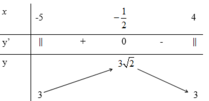
M=(x+3)(x+9)
Với mọi x là số tự nhiên là hợp lí
VD:0;1;2;..