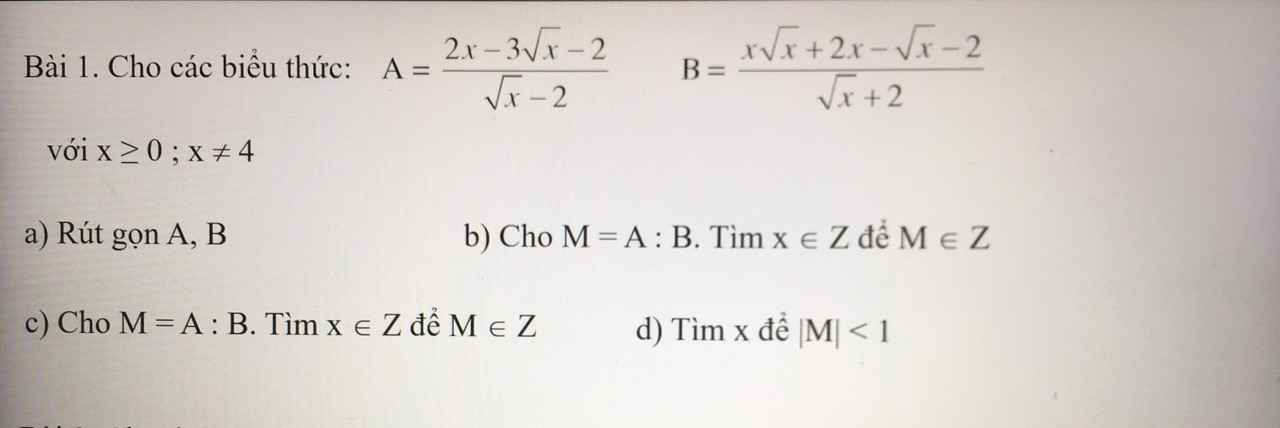giải hộ minh với
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HA
1
14 tháng 10 2021
\(a,ĐK:x\ge0;x\ne4\\ A=\dfrac{\left(2\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\sqrt{x}-2}=2\sqrt{x}+1\\ B=\dfrac{\left(x-1\right)\left(\sqrt{x}+2\right)}{\sqrt{x}+2}=x-1\\ b,M=A:B=\dfrac{2\sqrt{x}+1}{x-1}=\dfrac{2\left(\sqrt{x}+1\right)-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ M=\dfrac{2}{\sqrt{x}-1}-\dfrac{1}{\sqrt{x}+1}\in Z\\ \Leftrightarrow\left\{{}\begin{matrix}\sqrt{x}-1\inƯ\left(2\right)=\left\{-2;-1;1;2\right\}\\\sqrt{x}+1\inƯ\left(1\right)=\left\{-1;1\right\}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\sqrt{x}\in\left\{0;2;3\right\}\left(\sqrt{x}\ge0\right)\\\sqrt{x}=0\left(\sqrt{x}\ge0\right)\end{matrix}\right.\Leftrightarrow x=0\)
28 tháng 12 2021
a, Ta có : abcabc + 7 > 1
Lại có : abcabc + 7
= abc . 1000 + abc . 1 + 7 = abc . 1001 + 7
= 7 . 143 . abc + 7 = 7 ( abc . 143 + 1 ) chia hết cho 7
Vì : 143 . abc + 1 thuộc N
=> abcabc + 7 chia hết cho 7
=> abcabc + 7 là hợp số
b,c, Tương tự câu a
DA
1
KN
15 tháng 3 2019
\(\frac{5}{2.1}+\frac{4}{1.11}+\frac{3}{11.12}+\frac{1}{2.15}+\frac{13}{15.4}\)
\(=\left(\frac{4}{1.11}+\frac{3}{11.12}\right)+\left(\frac{1}{2.15}+\frac{13}{15.4}\right)+\frac{5}{2.1}\)
\(=\frac{1}{11}\left(4+\frac{1}{4}\right)+\frac{1}{15}\left(\frac{1}{2}+\frac{13}{4}\right)+\frac{5}{2.1}\)
\(=\frac{1}{11}.\frac{17}{4}+\frac{1}{15}.\frac{17}{4}+\frac{5}{2}\)
\(=\frac{17}{4}\left(\frac{1}{11}+\frac{1}{15}\right)+\frac{5}{2}\)
\(=\frac{17}{4}.\frac{26}{165}+\frac{5}{2}\)
\(=\frac{442}{660}+\frac{5}{2}\)
\(=\frac{221}{330}+\frac{825}{330}\)
\(=\frac{1046}{330}\)
\(=\frac{523}{165}\)
17 tháng 10 2017
n nhân (n công 1)=n nhân 1 nhân n công 1=n nhân (1+1)=n nhan 2 chia hết cho2
H
2
KV
9 tháng 10 2023
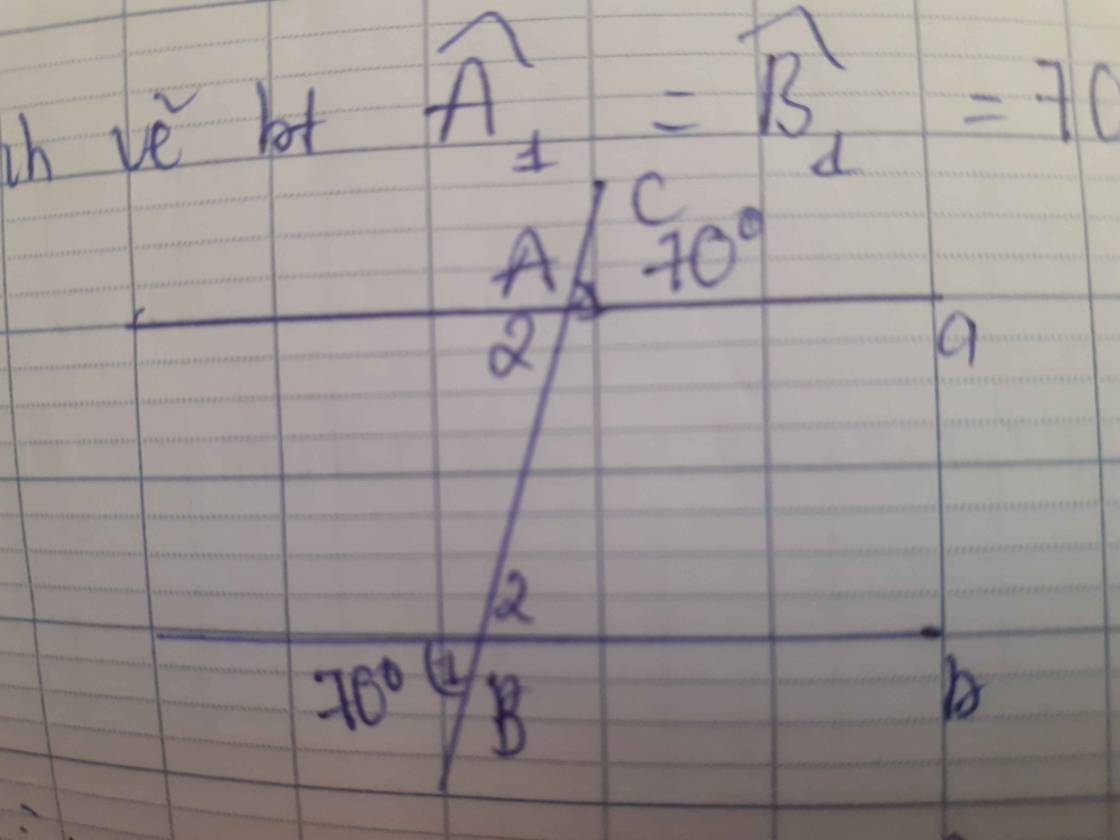
Ta có:
∠B₂ = ∠B₁ = 70⁰ (đối đỉnh)
⇒ ∠B₂ = ∠A₁ = 70⁰
Mà ∠B₂ và ∠A₁ là hai góc đồng vị
⇒ a // b
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 4 2021
TH1: \(m=-1\) thỏa mãn (dễ dàng kiểm tra các giá trị \(f\left(-1\right)>0\) ; \(f\left(0\right)< 0\) ; \(f\left(3\right)>0\) nên pt có ít nhất 2 nghiệm thuộc (-1;0) và (0;3)
TH2: \(m>-1\):
\(\lim\limits_{x\rightarrow+\infty}f\left(x\right)=\lim\limits_{x\rightarrow+\infty}x^4\left[m\left(1-\dfrac{2}{x}\right)^2\left(1+\dfrac{9}{x}\right)+1-\dfrac{32}{x^4}\right]=+\infty.\left(m+1\right)=+\infty>0\)
\(\Rightarrow\) Luôn tồn tại 1 giá trị \(x=a\) đủ lớn sao cho \(f\left(a\right)>0\)
\(f\left(0\right)=-32< 0\Rightarrow f\left(a\right).f\left(0\right)< 0\)
\(\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm dương
\(f\left(-9\right)=9^4-32>0\Rightarrow f\left(-9\right).f\left(0\right)< 0\)
\(\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm âm thuộc \(\left(-9;0\right)\)
\(\Rightarrow f\left(x\right)\) luôn có ít nhất 2 nghiệm
TH3: \(m< -1\) tương tự ta có: \(\lim\limits_{x\rightarrow+\infty}f\left(x\right)=\lim\limits_{x\rightarrow-\infty}=+\infty.\left(m+1\right)=-\infty\)
\(\Rightarrow\) Luôn tồn tại 1 giá trị \(x=a>0\) đủ lớn và \(x=b< 0\) đủ nhỏ sao cho \(\left\{{}\begin{matrix}f\left(a\right)< 0\\f\left(b\right)< 0\end{matrix}\right.\)
Lại có \(f\left(-9\right)=9^4-32>0\) \(\Rightarrow\left\{{}\begin{matrix}f\left(-9\right).f\left(a\right)< 0\\f\left(-9\right).f\left(b\right)< 0\end{matrix}\right.\)
\(\Rightarrow\) Pt luôn có ít nhất 2 nghiệm thuộc \(\left(-\infty;-9\right)\) và \(\left(-9;+\infty\right)\)
Vậy pt luôn có ít nhất 2 nghiệm với mọi m
CB
14 tháng 7 2016
\(2x+69\times2=69\times4\)
\(2x+138=276\)
\(2x=276-138\)
\(2x=138\)
\(x=138:2\)
\(x=69\)
T ủng hộ mk nha ^...^ ^_^
XO
4 tháng 12 2020
Ta có \(\frac{bz-cy}{a}=\frac{cx-az}{b}=\frac{ay-bx}{c}\)
=> \(\frac{abz-acy}{a^2}=\frac{bcx-baz}{b^2}=\frac{cay-cbx}{c^2}=\frac{abz-acy+bcx-baz+cay-cbx}{a^2+b^2+c^2}\)
\(=\frac{0}{a^2+b^2+c^2}=0\)
=> \(\hept{\begin{cases}bz-cy=0\\cx-az=0\\ay-bx=0\end{cases}}\Rightarrow\hept{\begin{cases}bz=cy\\cx=az\\ay=bx\end{cases}}\Rightarrow\hept{\begin{cases}\frac{z}{c}=\frac{y}{b}\\\frac{z}{c}=\frac{x}{a}\\\frac{y}{b}=\frac{x}{a}\end{cases}}\Rightarrow\frac{x}{a}=\frac{y}{b}=\frac{z}{c}\left(\text{đpcm}\right)\)