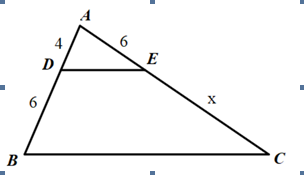
Cho hình vẽ, biết ΔABC có DE=BC , AB = 4cm , DB = 6cm AE = 6cm . Tìm x
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: AC-BC<AB<AC+BC
=>5<AB<8
mà AB>6
nên AB=7cm
b: AB-AC<BC<AB+AC
=>2<BC<14
mà BC<4
nên BC=3cm

Gọi O là tâm đường tròn ngoại tiếp ΔABC
Gọi H là giao của AO với BC
AB=AC
OB=OC
Do đó: AO là trung trực của BC
=>AH là trung trực của BC
=>H là trung điểm của BC
HB=HC=4/2=2cm
Kẻ giao của AO với (O) là D
=>AD là đường kính của (O)
Xét (O) có
ΔABD nội tiếp
ADlà đường kính
Do đó: ΔBAD vuông tại B
ΔAHB vuông tại H
=>AH^2+HB^2=AB^2
=>\(AH^2=6^2-2^2=32\)
=>\(AH=4\sqrt{2}\left(cm\right)\)
Xét ΔBAD vuông tại B có BH là đường cao
nên AB^2=AH*AD
=>\(AD=\dfrac{6^2}{4\sqrt{2}}=\dfrac{9}{\sqrt{2}}\left(cm\right)\)
=>\(R=\dfrac{AD}{2}=\dfrac{9}{2\sqrt{2}}\left(cm\right)\)

a: BC=10cm
Xét ΔABC có AD là phân giác
nên BD/CD=AB/AC=3/4
=>BD/3=CD/4
Áp dụng tính chất của dãy tỉ số bằng nhau,ta được:
\(\dfrac{BD}{3}=\dfrac{CD}{4}=\dfrac{BD+CD}{3+4}=\dfrac{10}{7}\)
Do đó: BD=30/7(cm); CD=40/7(cm)
b: Xét ΔABC có DE//AC
nên DE/AC=BD/BC
=>\(\dfrac{DE}{8}=\dfrac{30}{7}:10=\dfrac{3}{7}\)
=>DE=24/7(cm)

a.Xét ΔABD và ΔIBD có:
BAD=BID=90 độ
BD chung
ABD=IBD (do BD là phân giác góc ABC)
=>ΔABD=ΔIBD (ch-gn)
b.Ta có: ΔABD=ΔIBD (cm câu a)
=>AB=IB (2 cạnh tương ứng)
=>ΔABI cân tại B
Lại có: BD là đường phân giác góc B
=>BD đồng thời là đường cao
=>BD⊥AI
c.Ta có: ΔABD=ΔIBD (cm câu a)
=>AD=ID (2 cạnh tương ứng)
Xét ΔDAK và ΔDIC có:
DAK=DIC (=90 độ)
DA=DI (cmt)
ADK=IDC (2 góc đối đỉnh)
=>ΔDAK=ΔDIC (g.c.g)
=>DK=DC (2 cạnh tương ứng)
d.Vì ΔABC vuông tại A nên:
=>BC²=AB²+AC²
<=>BC²=6²+8²
<=>BC²=100
<=>BC=√100=10 (cm)
Ta có: BI+IC=BC
=>IC=BC-BI
Lại có: AB=BI (cm câu b)
=>IC=BC-AB
=>IC=10-6=4 (cm)
Vậy IC=4 cm.

Xét tam giác \(ABC\) có \(DE//BC\) nên theo định lí Thales ta có:
\(\frac{{AD}}{{BD}} = \frac{{AE}}{{EC}} \Rightarrow \frac{x}{2} = \frac{6}{3}\). Do đó, \(x = \frac{{6.2}}{3} = 4\).
Vậy \(x = 4\).

Ta có:
\(AB^2=4^2=16\)
\(AC^2=6^2=36\)
\(BC^2=\left(2\sqrt{13}\right)^2=52\)
\(\Rightarrow AB^2+AC^2=BC^2\left(=52\right)\)
\(\Rightarrow\Delta ABC\) vuông tại A (theo định lý Pytago đảo)
\(\Rightarrow sinB=\dfrac{AC}{BC}\)
\(sinC=\dfrac{AB}{BC}\)
\(\Rightarrow\dfrac{sinB}{sinC}=\dfrac{\dfrac{AC}{BC}}{\dfrac{AB}{BC}}=\dfrac{AC}{AB}\)
\(\Rightarrow AB.sinB=AC.sinC\)
\(DE=EC\\ \Rightarrow DE//BC\\ \Rightarrow\dfrac{AD}{DB}=\dfrac{AE}{EC}\Rightarrow\dfrac{4}{6}=\dfrac{6}{x}\\ \Rightarrow x=9\)
hấy sai sai sao ý ;-;