Mọi người giúp Mình làm câu 2 nha cảm ơn mọi người 😊
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NT
1
Những câu hỏi liên quan
BG
19 tháng 7 2021
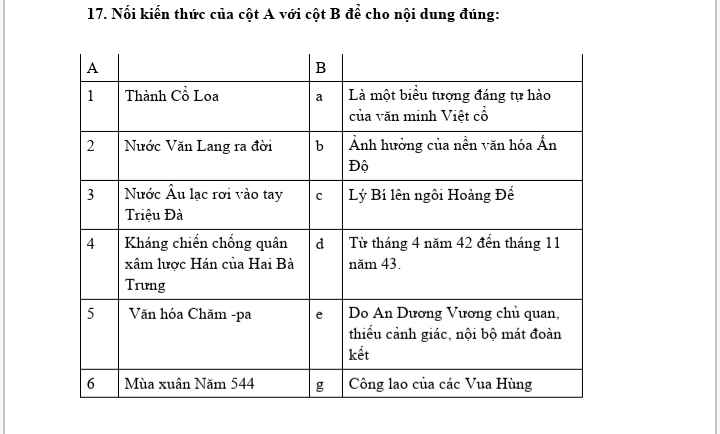
1.a
2. g
3.e
4.d
5.b
6.c
II. Tự luận
1. Năm 938, quân Nam Hán kéo vào bờ biển nước ta, lúc này nước triều đang dâng, quân ta khiêu chiến giả vờ thua rút chạy, giặc đuổi theo vượt qua bãi cọc ngầm nên bị đắm thuyền.
- Đây là chiến thắng lẫy lừng của dân tộc ta, đã đánh bại hoàn toàn ý chí xâm lược của nhà Nam Hán.
2. Cuộc khởi nghĩa Mai Thúc Loan ( năm 722 ).
- Cuộc khởi nghĩa Phùng Hưng ( năm 776-794 ).
- Cuộc khởi nghĩa Khúc Thừa Dụ ( năm 905 ).
- Cuộc khởi nghĩa chống quân Nam Hán lần thứ nhất của Dương Đình Nghệ ( năm 930-931 ).
- Cuộc khởi nghĩa cống quân Nam Hán lần thứ hai của Ngô Quyền (năm 938).
- Khởi nghĩa Lý Tự Tiên và Đinh Kiến (687), khởi nghĩa Mai Thúc Loan (722), khởi nghĩa Phùng Hưng (766-791), khởi nghĩa Dương Thanh (819-820).
3. Chủ động đón đánh quân xâm lược, bố trí bãi cọc ngầm lợi dụng thủy triều, sử dụng thuyền nhỏ dụ địch và dễ luồn lách ở bãi cọc nhọn.
- Chủ động: đón đánh quân xâm lược bằng cách bố trí lực lượng hùng mạnh và xây dựng bãi cọc ngầm trên sông Bạch Đằng.
- Độc đáo : Lợi dụng thủy triều, xây dựng bãi cọc ngầm với hàng nghìn cọc nhọn, chỉ sử dụng thuyền nhỏ để dễ luồn lách.
2Q
2
4 tháng 11 2021
Câu 1.
a) Vì hai điện tích cùng dấu nên lực tương tác của chúng là đẩy nhau.
b) Lực tương tác:
\(F=k\cdot\dfrac{\left|q_1\cdot q_2\right|}{r^2}=9\cdot10^9\cdot\dfrac{6\cdot10^{-4}\cdot4\cdot10^{-5}}{0,06^2}=60000N\)
Câu 2.
a)Lực tương tác:
\(F=k\cdot\dfrac{\left|q_1\cdot q_2\right|}{r^2}=9\cdot10^9\cdot\dfrac{q^2}{0,03^2}=4\cdot10^{-2}\)
\(\Rightarrow q_1=q_2=q=6,32\cdot10^{-8}C\)
b)Để lực tương tác là \(8\cdot10^{-2}N\) cần đặt hai điện tích:
\(F'=k\cdot\dfrac{\left|q_1q_2\right|}{r'^2}=9\cdot10^9\cdot\dfrac{4\cdot10^{-15}}{r'^2}=8\cdot10^{-2}\)
\(\Rightarrow r'\approx0,02m=2cm\)
4 tháng 11 2021
Câu 1:
a)Lực đẩy vì điện tích giữa chúng là cùng dấu
b)\(F=\dfrac{k\left|q_1q_2\right|}{r^2}=\dfrac{9.10^9\left|6.10^{-4}.4.10^{-5}\right|}{0,06^2}=3600\left(N\right)\)
4 tháng 5 2021
Câu 1:
const fi='dulieu.dat';
fo='thaythe.out';
var f1,f2:text;
a:array[1..100]of string;
n,d,i,vt:integer;
begin
assign(f1,fi); reset(f1);
assign(f2,fo); rewrite(f2);
n:=0;
while not eof(f1) do
begin
n:=n+1;
readln(f1,a[n]);
end;
for i:=1 to n do
begin
d:=length(a[i]);
vt:=pos('anh',a[i]);
while vt<>0 do
begin
delete(a[i],vt,3);
insert('em',a[i],vt);
vt:=pos('anh',a[i]);
end;
end;
for i:=1 to n do
writeln(f2,a[i]);
close(f1);
close(f2);
end.
4 tháng 5 2021
Câu 2:
uses crt;
const fi='mang.inp';
fo='sapxep.out';
var f1,f2:text;
a:array[1..100]of integer;
i,n,tam,j:integer;
begin
clrscr;
assign(f1,fi); rewrite(f1);
assign(f2,fo); rewrite(f2);
write('Nhap n='); readln(n);
for i:=1 to n do
begin
write('A[',i,']='); readln(a[i]);
end;
for i:=1 to n do
write(f1,a[i]:4);
for i:=1 to n-1 do
for j:=i+1 to n do
if a[i]>a[j] then
begin
tam:=a[i];
a[i]:=a[j];
a[j]:=tam;
end;
for i:=1 to n do
write(f2,a[i]:4);
close(f1);
close(f2);
end.
L
cảm ơn mọi người nhiều...
1
17 tháng 2 2021
Do M là điểm chính giữa của cung AB \(\Rightarrow MA=MB\) (1)
Ta có \(\Lambda MAN=\Lambda MAB=\dfrac{1}{2}sđcungMB\) (\(\Lambda\) kí hiệu góc)
\(\Lambda MBC=\dfrac{1}{2}sđcungMB\) \(\Rightarrow\Lambda MAN=\Lambda MBC\)(2)
\(\Lambda AMN\) là góc chắn đường kính AB \(\Rightarrow\Lambda AMB=90^0\Rightarrow\Lambda AMN+\Lambda NMB=90^0\)
\(\Lambda NMC=90^0\Rightarrow\Lambda NMB+\Lambda BMC=90^0\) \(\Rightarrow\Lambda AMN=\Lambda BMC\)(3)
Từ (1) ,(2) và (3) \(\Rightarrow\Delta AMN=\Delta BMC\left(g.c.g\right)\)
14 tháng 8 2021
Bài 1 :
\(\frac{x}{2}=\frac{y}{3};\frac{y}{4}=\frac{z}{5}\Rightarrow\frac{x}{8}=\frac{y}{12}=\frac{z}{15}\)
Theo tính chất dãy tỉ số bằng nhau
\(\frac{x}{8}=\frac{y}{12}=\frac{z}{15}=\frac{x+y-z}{8+12-15}=\frac{10}{5}=2\Rightarrow x=16;y=24;z=30\)
bài 2 :
Đặt \(x=2k;y=5k\Rightarrow xy=10k^2=10\Leftrightarrow k^2=1\Leftrightarrow k=\pm1\)
Với k = 1 thì x = 2 ; y = 5
Với k = - 1 thì x = -2 ; y = -5
TH
0
NV
5
12 tháng 4 2021
4: Đặt \(x=\dfrac{a+b}{a-b};y=\dfrac{b+c}{b-c};z=\dfrac{c+a}{c-a}\).
Ta có \(\left(x+1\right)\left(y+1\right)\left(z+1\right)=\dfrac{2a.2b.2c}{\left(a-b\right)\left(b-c\right)\left(c-a\right)}=\left(x-1\right)\left(y-1\right)\left(z-1\right)\)
\(\Rightarrow xy+yz+zx=-1\).
Bất đẳng thức đã cho tương đương:
\(x^2+y^2+z^2\ge2\Leftrightarrow\left(x+y+z\right)^2-2\left(xy+yz+zx\right)-2\ge0\Leftrightarrow\left(x+y+z\right)^2\ge0\) (luôn đúng).
Vậy ta có đpcm
12 tháng 4 2021
mình xí câu 45,47,51 :>
45. a) Áp dụng bất đẳng thức Cauchy-Schwarz dạng Engel ta có :
\(\dfrac{1}{a}+\dfrac{2}{b}=\dfrac{1}{a}+\dfrac{4}{2b}\ge\dfrac{\left(1+2\right)^2}{a+2b}=\dfrac{9}{a+2b}\left(đpcm\right)\)
Đẳng thức xảy ra <=> a=b
b) Áp dụng bất đẳng thức Cauchy-Schwarz dạng Engel ta có :
\(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{b}\ge\dfrac{\left(1+1+1\right)^2}{a+b+b}=\dfrac{9}{a+2b}\)(1)
\(\dfrac{1}{b}+\dfrac{1}{c}+\dfrac{1}{c}\ge\dfrac{\left(1+1+1\right)^2}{b+c+c}=\dfrac{9}{b+2c}\)(2)
\(\dfrac{1}{c}+\dfrac{1}{a}+\dfrac{1}{a}\ge\dfrac{\left(1+1+1\right)^2}{c+a+a}=\dfrac{9}{c+2a}\)(3)
Cộng (1),(2),(3) theo vế ta có đpcm
Đẳng thức xảy ra <=> a=b=c
3:
=3,45(123+4-27)
=3,45*100=345
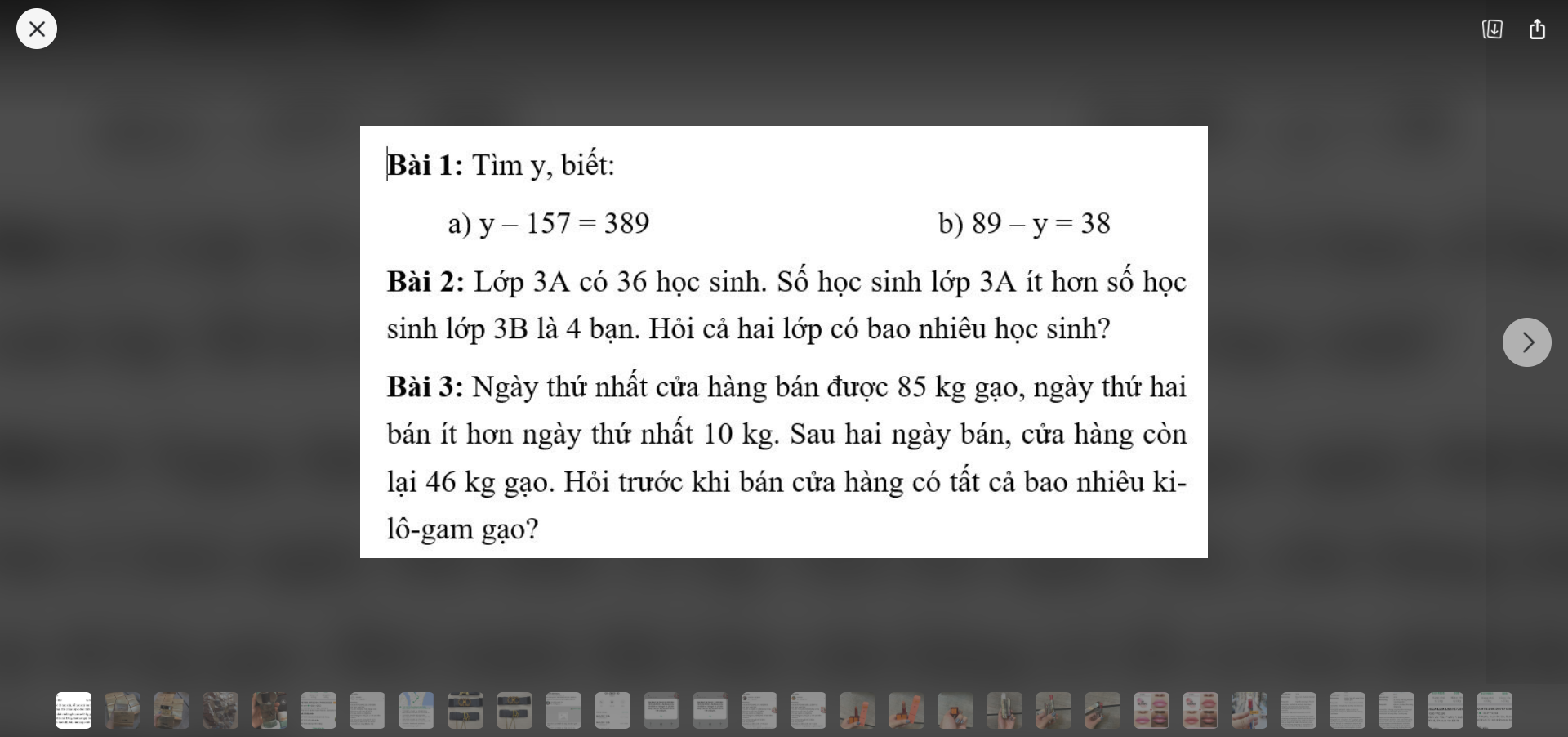
2:
a: thể tích của bể là;
18*12*15=3240 lít
b: Hiện tại bể đang chứa:
3240*0,5=1620 lít