Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì tam giác ABC cân tại A có đường cao AH nên D là trung điểm BC
Từ C kẻ đường thẳng vuông góc với BC cắt AB tại G
\(\Rightarrow CG\parallel AD\) mà D là trung điểm BC \(\Rightarrow A\) là trung điểm BG
nên AD là đường trung bình tam giác BCG \(\Rightarrow AD=\dfrac{CG}{2}\)
\(\Rightarrow2AD=CG\Rightarrow4AD^2=CG^2\)
tam giác BCG vuông tại C có đường cao CF nên áp dụng hệ thức lượng
\(\Rightarrow\dfrac{1}{BC^2}+\dfrac{1}{CG^2}=\dfrac{1}{CF^2}\Rightarrow\dfrac{1}{BC^2}+\dfrac{1}{4AD^2}=\dfrac{1}{CF^2}\)
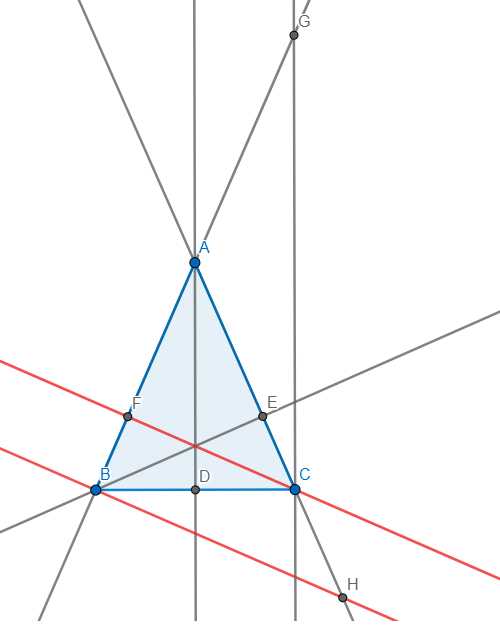

a,Xét tg DHB và tg DCA có: ^HDB=^CDA=90 độ, ^DBH=^DAC ( cùng phụ với hai góc bằng nhau BHD=^AHE)
Do đó: tg HDB đồng dạng tg DCA (g.g)
Suy ra: HD/DC=BD/DA-> bd*dc=dh*da
b, HD/HA=SBHC/SABC
HE/BE=SAHC/SABC
HF/CF=SHAB/SABC
HD/HA+HE/BE+HF/CF=SBHC/SABC+SAHC/SABC+SAHB/SABC=1

a: Xét ΔHFA vuông tại F và ΔHDC vuông tại D có
\(\widehat{FHA}=\widehat{DHC}\)(hai góc đối đỉnh)
Do đó: ΔHFA~ΔHDC
=>\(\dfrac{HF}{HD}=\dfrac{HA}{HC}\)
=>\(HF\cdot HC=HD\cdot HA\left(1\right)\)
Xét ΔHFB vuông tại F và ΔHEC vuông tại E có
\(\widehat{FHB}=\widehat{EHC}\)(hai góc đối đỉnh)
Do đó: ΔHFB~ΔHEC
=>\(\dfrac{HF}{HE}=\dfrac{HB}{HC}\)
=>\(HF\cdot HC=HB\cdot HE\left(2\right)\)
Từ (1) và (2) suy ra \(HA\cdot HD=HF\cdot HC=HB\cdot HE\)
c: Xét tứ giác AFHE có \(\widehat{AFH}+\widehat{AEH}=90^0+90^0=180^0\)
nên AFHE là tứ giác nội tiếp
Xét tứ giác BFHD có \(\widehat{BFH}+\widehat{BDH}=90^0+90^0=180^0\)
nên BFHD là tứ giác nội tiếp
Xét tứ giác CEHD có \(\widehat{CEH}+\widehat{CDH}=90^0+90^0=180^0\)
nên CEHD là tứ giác nội tiếp
Ta có: \(\widehat{EFH}=\widehat{EAH}\)(AEHF là tứ giác nội tiếp)
\(\widehat{DFH}=\widehat{DBH}\)(BFHD là tứ giác nội tiếp)
mà \(\widehat{EAH}=\widehat{DBH}\left(=90^0-\widehat{ECB}\right)\)
nên \(\widehat{EFH}=\widehat{DFH}\)
=>FH là phân giác của góc EFD
Ta có: \(\widehat{FEH}=\widehat{FAH}\)(AEHF là tứ giác nội tiếp)
\(\widehat{DEH}=\widehat{DCH}\)(ECDH là tứ giác nội tiếp)
mà \(\widehat{FAH}=\widehat{DCH}\left(=90^0-\widehat{ABD}\right)\)
nên \(\widehat{FEH}=\widehat{DEH}\)
=>EH là phân giác của góc FED
Xét ΔFED có
EH,FH là các đường phân giác
Do đó: H là giao điểm của ba đường phân giác trong ΔFED

Xét ∆ABE và ∆ACF có:
\(\widehat{A}\left(chung\right)\)
\(\widehat{AEB}=\widehat{AFC}\left(=90^0\right)\)
\(\Rightarrow\)∆ABE ~ ∆ACF (g-g)
\(\Rightarrow\frac{AE}{AF}=\frac{AB}{AC}\Rightarrow\frac{AE}{AB}=\frac{AF}{AC}\)
Xét ∆AEF và ∆ABC có:
\(\frac{AE}{AB}=\frac{AF}{AC}\left(cmt\right)\)
\(\widehat{A}\left(chung\right)\)\
\(\Rightarrow\)∆AEF ~ ∆ABC (đpcm)
Ta có: \(\tan B=\frac{ÁD}{DB};\tan C=\frac{AD}{DC}\)
Xét ∆ADC và ∆BDH có:
\(\widehat{HBD}=\widehat{CAD}\)( cùng phụ với \(\widehat{C}\))
\(\widehat{ADC}=\widehat{BDH}\left(=90^0\right)\)
\(\Rightarrow\)∆ADC ~ ∆ BDH (g-g)
\(\Rightarrow\frac{AD}{DC}=\frac{BD}{DH}\)
\(\Rightarrow\tan B\cdot\tan C=\frac{AD}{DB}\cdot\frac{AD}{DC}=\frac{AD}{DB}\cdot\frac{BD}{DH}=\frac{AD}{DH}\)(đpcm)
 đó nha bn
đó nha bn