cho tam giác ABC có S=2, đường thẳng AB có phương trình x-y=0. Biết I(2;1) là trung điểm của BC. Tìm tọa độ trung điểm của AC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tọa độ A là nghiệm: \(\left\{{}\begin{matrix}x-y-2=0\\x+2y-5=0\end{matrix}\right.\) \(\Rightarrow A\left(3;1\right)\)
\(\left\{{}\begin{matrix}x_A+x_B+x_C=3x_G\\y_A+y_B+y_C=3y_G\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_B+x_C=6\\y_B+y_C=5\end{matrix}\right.\) (1)
B thuộc AB nên: \(x_B-y_B=2\Rightarrow x_B=y_B+2\)
C thuộc AC nên: \(x_C+2y_C-5=0\Rightarrow x_C=-2y_C+5\)
Thế vào (1) \(\Rightarrow\left\{{}\begin{matrix}y_B+2-2y_C+5=6\\y_B+y_C=5\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}y_B=3\Rightarrow x_B=5\\y_C=2\Rightarrow x_C=1\end{matrix}\right.\)
Phương trình BC: \(\dfrac{x-5}{1-5}=\dfrac{y-3}{2-3}\Leftrightarrow x-4y+7=0\)

ta có tọa độ B là nghiệm của hệ \(\hept{\begin{cases}x-2=0\\2x+3y=1\end{cases}\Leftrightarrow B\left(2;-1\right)}\)
Từ I kẻ d' qua I và song song với BC khi đó \(d':x=-7\)
Khi đó d' cắt AC tại điểm K có tọa độ là \(\hept{\begin{cases}x=-7\\2x+3y=1\end{cases}\Leftrightarrow}K\left(-7;5\right)\), gọi H là trung điểm của BC
khi đó điểm A thuộc trung trực của KI là đường thẳng AH: \(y=1\)Do đó tọa độ A là : \(A\left(-1;1\right)\)
Do đó đường cao từ C có VTPT \(IA=\left(6,4\right)\)nên đường cao từ C là : \(3x+2y-4=0\)

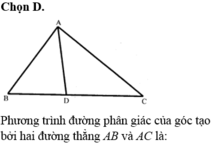
Đáp án B
Do AB và BC cắt nhau tại B nên toa độ điểm B là nghiệm hệ phương trình

Do đó: B( 2; -1)
Tương tự: tọa độ điểm C( 1; 9)
PT các đường phân giác góc A là:
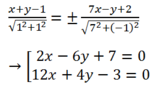
Đặt T1(x; y) = 2x- 6y+ 7 và T2= 12x+ 4y-3 ta có:
T1(B). T1(C) < 0 và T2(B) T2(C) >0.
Suy ra B và C nằm khác phía so với đường thẳng 2x-6y+7= 0 và cùng phía so với đường thẳng: 12x+ 4y- 3= 0.
Vậy phương trình đường phân giác trong góc A là: 2x- 6y+ 7= 0.



Gọi K là trung điểm AC \(\Rightarrow IK\) là đường trung bình tam giác ABC
\(\Rightarrow\left\{{}\begin{matrix}IK=\dfrac{1}{2}AB\\IK||AB\end{matrix}\right.\)
Đường thẳng IK song song AB nên nhận (1;-1) là 1 vtpt
Phương trình IK:
\(1\left(x-2\right)-1\left(y-1\right)=0\Leftrightarrow x-y-1=0\)
\(S=\dfrac{1}{2}d\left(C;AB\right).AB=\dfrac{1}{2}.2.d\left(I;AB\right).AB=d\left(I;AB\right).AB\)
\(\Rightarrow AB=\dfrac{S}{d\left(I;AB\right)}=\dfrac{2}{\dfrac{\left|2-1\right|}{\sqrt{1^2+\left(-1\right)^2}}}=2\sqrt{2}\)
\(\Rightarrow IK=\dfrac{1}{2}AB=\sqrt{2}\)
Do K thuộc IK nên tọa độ có dạng: \(K\left(k;k-1\right)\Rightarrow\overrightarrow{IK}=\left(k-2;k-2\right)\)
\(\Rightarrow IK=\sqrt{\left(k-2\right)^2+\left(k-2\right)^2}=\sqrt{2}\)
\(\Rightarrow\left(k-2\right)^2=1\Rightarrow\left[{}\begin{matrix}k=3\\k=1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}K\left(3;2\right)\\K\left(1;0\right)\end{matrix}\right.\)