Cho tam giác ABC vuông tại A . Gọi M là d' nằm bên trong của tam giác đó. Chứng minh <BMc là góc tù
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 1 2016
đố ai giải được bài toán khó lớp 7 này đấy (em trong đội tuyển hsg toán nè!)
5 tháng 4 2019
Đề bài thiếu, nếu ABC là tam giác vuông bất kì thì không thể chứng minh ACD là tam giác cân được. ABC phải là tam giác vuông cân.
Câu hỏi này đã có trả lời ở đây: https://olm.vn/hoi-dap/detail/185970928943.html
5 tháng 4 2019
Câu hỏi của linh ngoc - Toán lớp 7 - Học toán với OnlineMath
16 tháng 12 2023
a: Xét ΔMAB và ΔMDC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔMAB=ΔMDC
b: Ta có: ΔMAB=ΔMDC
=>\(\widehat{MAB}=\widehat{MDC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CD
Ta có: AB//CD
AB\(\perp\)AC
Do đó: CD\(\perp\)CA
Xét ΔABC vuông tại A và ΔCDA vuông tại C có
AB=CD
AC chung
Do đó: ΔABC=ΔCDA
c: Ta có: ΔABC=ΔCDA
=>BC=DA
Xét ΔMCA và ΔMBD có
MC=MB
\(\widehat{CMA}=\widehat{BMD}\)(hai góc đối đỉnh)
MA=MD
Do đó: ΔMCA=ΔMBD
=>\(\widehat{MCA}=\widehat{MBD}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AC//BD
Ta có: AC//BD
AC\(\perp\)CD
Do đó: DC\(\perp\)DB
=>ΔDBC vuông tại D
31 tháng 12 2023
a: Xét ΔMBD vuông tại M và ΔNCE vuông tại N có
DB=EC
\(\widehat{DBM}=\widehat{ECN}\)(ΔABC cân tại A)
Do đó: ΔMBD=ΔNCE
b: Ta có: ΔMBD=ΔNCE
=>MB=NC
Ta có: AM+MB=AB
AN+NC=AC
mà MB=NC và AB=AC
nên AM=AN
Xét ΔAMK vuông tại M và ΔANK vuông tại N có
AK chung
AM=AN
Do đó: ΔAMK=ΔANK
CM
25 tháng 8 2017
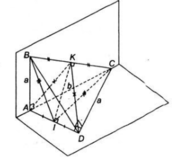
Chứng minh tương tự, ta có tam giác AKD là tam giác cân tại K có KI là đường trung tuyến nên đồng thời là đường cao.
⇒ IK ⊥ AD (2)
Từ (1) và (2) suy ra; IK là đường vuông góc chung của hai đường thẳng AD và BC.
NK
8 tháng 9 2019
A B C H K D E F M
Em tài trợ cái hình cho mọi người dễ nhìn ạ!
NK
8 tháng 9 2019
à, cái chỗ đoạn thẳng H, A, D là đường đứt khúc ạ, em quên sửa!