cho tam giác ABC vuông tại A, đường cao AH, biết AB = 5cm, AC =12cm, tia phân giác của góc ABC cắt AH và AC theo thứ tự E và F
Tính BC, AF, FC?
Giúp tui với mọi người
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 4 2018
Ta có: \(AB.FC=BC.AE\Rightarrow\frac{AB}{AE}=\frac{BC}{FC}\)
\(\widehat{AB}F+\widehat{BAH}=90^0;\widehat{ABC}+\widehat{C}=90^0\Rightarrow\widehat{C}=\widehat{BAH}\)
Xét tam giác ABE và tam giác CBF ta có:
\(\widehat{ABE}=\widehat{FBC}\)( BF là tia phân giác )
\(\widehat{BAH}=\widehat{C}\left(cmt\right)\)
\(\Rightarrow\Delta ABE~CBF\left(g-g\right)\)
\(\Rightarrow\frac{AB}{BC}=\frac{AE}{FC}\Rightarrow AB.FC=BC.AE\)
BC). Tia phân giác của góc ABC cắt AH tại E và cắt AC tại F.
8 tháng 4 2022
a)Xét △ABC vuông tại A (gt)
=> BC2 = AB2 + AC2 (định lý Pytago)
BC2 = 52 + 122 = 25 + 144 = 169
=> BC = \(\sqrt{169}\) = 13 cm
Xét △ABC có BF là tia phân giác của góc ABC (gt)
=>\(\dfrac{AF}{AB}\) = \(\dfrac{FC}{BC}\) (tính chất đường phân giác)
=>\(\dfrac{AF}{5}\) = \(\dfrac{FC}{13}\) và AF + FC = AC = 12
Áp dụng tính chất dãy tỉ số bằng nhau ta được:
\(\dfrac{AF}{5}\) = \(\dfrac{FC}{13}\) = \(\dfrac{AF+FC}{5+13}\) = \(\dfrac{AC}{18}\) = \(\dfrac{2}{3}\)
=> AF = \(\dfrac{2}{3}\) x 5 = 3,33 cm và FC = \(\dfrac{2}{3}\) x 13 = 8,67 cm
b)Xét △ABF và △HBE có:
góc ABF bằng góc HBE (BF là tia phân giác của góc ABC)
góc BAF bằng góc BHE bằng 90o (tam giác ABC vuông tại A và AH ⊥ BC)
=> △ABF ∼ △HBE (g.g)
c) Vì △ABF ∼ △HBE (câu b)
=> góc BFA bằng góc BEH
mà góc AEF bằng góc BEH (2 góc đối đỉnh)
=> góc BFA bằng góc AEF
=> △AEF cân tại A
d)Xét △ABC và △AHB có:
góc ABC chung
góc BAC bằng góc BHA bằng 90o (tam giác ABC vuông tại A và AH ⊥ BC)
=> △ABC ∼ △HBA (g.g)
=> \(\dfrac{AB}{BC}\) = \(\dfrac{BH}{AB}\) (1)
Xét △ABH có BE là tia phân giác của góc ABC (gt)
=>\(\dfrac{HE}{AE}\) = \(\dfrac{BH}{AB}\) (2) (tính chất đường phân giác)
Từ (1), (2) => \(\dfrac{AB}{BC}\) = \(\dfrac{HE}{AE}\)
=> AB.AE=BC.HE(chắc vậy?)
13 tháng 6 2020
a)
+) \(\Delta\)ABC vuông tại A
theo định lí pitago => \(BC=\sqrt{AB^2+AC^2}=13\)
+) BF là tia phân giác ^ABC
Theo tích chất phân giác: \(\frac{AF}{CF}=\frac{AB}{CB}=\frac{5}{13}\)
=> \(\frac{AF}{5}=\frac{CF}{13}=\frac{AF+CF}{5+13}=\frac{12}{18}=\frac{2}{3}\)
=> AF = 10/3 và CF = 26/3
b) Xét \(\Delta\)ABF và \(\Delta\)HBE có: ^ABF = ^HBE ( tích chất phân giác ) và ^FAB = ^EHB = 90 độ
=> \(\Delta\)ABF ~ \(\Delta\)HBE
c) (b) => ^BEH = ^BFA mà ^BEH = ^AEF ( đối đỉnh)
=> ^AEF = ^BFA = ^EFA
=> \(\Delta\)AEF cân
6 tháng 3 2023
4:
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
b Xét ΔABC vuông tại A có AH là đường cao
nen AH^2=HB*HC
c: BC=căn 6^2+8^2=10(cm)
=>AH=6*8/10=4,8cm
29 tháng 6 2023
a: BC=căn 6^2+8^2=10cm
BF là phân giác
=>FA/AB=FC/BC
=>FA/3=FC/5=(FA+FC)/(3+5)=8/8=1
=>FA=3cm; FC=5cm
b: Xét ΔABC vuông tại A và ΔHAC vuông tại H có
góc C chung
=>ΔABC đồng dạng với ΔHAC
L
14 tháng 12 2021
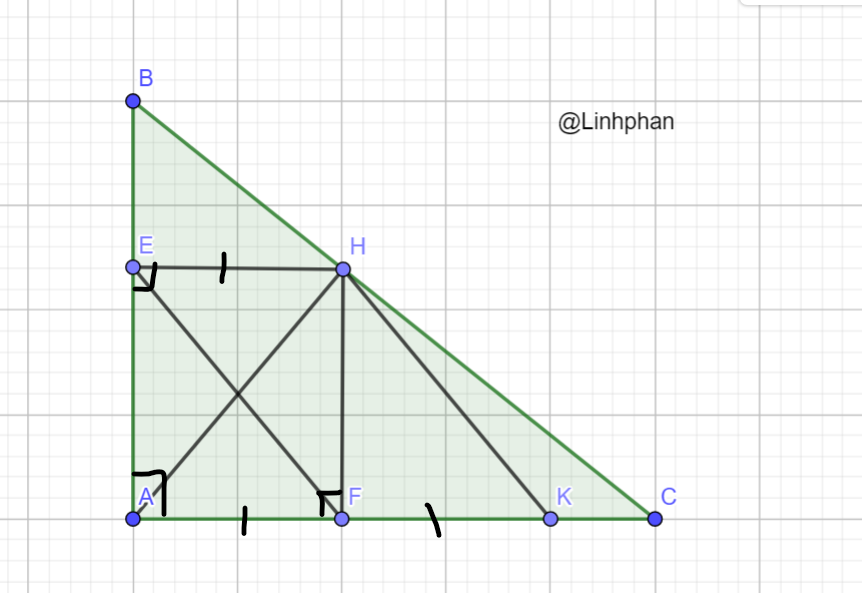
a, Vì HE ⊥ AB ; FA ⊥ AB => HE // FA (từ ⊥ đến // )
+, EA ⊥ AC ; HF ⊥ AC => EA // HF (từ ⊥ đến // )
Xét tứ giác AEHF có: HE // FA (cmt) ; EA // HF (cmt)
=> Tứ giác AEHF là hình bình hành (dhnb)
mà \(\hat{EAF} =90^0\)
=> Tứ giác AEHF là hình chữ nhật
=> AH = EF
b, Vì AEHF là hình chữ nhật (cmt)
=> EH//AF; EH = AF mà AF= FK (gt)
=> EH = FK
+, Xét tứ giác EHKF có: EH = FK (cmt)
EH // FK (do EH // AF; K ∈ AF)
=> Tứ giác EHKF là hình bình hành (dhnb)
\(\Delta ABC\)vuông, áp đụng Pytagore:
\(BC=\sqrt{AB^2+AC^2}=\sqrt{5^2+12^2}=\sqrt{169}=13cm\)
\(\Delta ABC\)tia phân giác góc B, áp dụng tính chất đường phân giác của một góc, dãy tỉ số bằng nhau:
\(\frac{AF}{AB}=\frac{FC}{BC}=\frac{AF+FC}{AB+BC}=\frac{AC}{5+13}=\frac{12}{18}=\frac{2}{3}\)
\(\Rightarrow AF=\frac{5.2}{3}=\frac{10}{3}cm\)
\(\Rightarrow FC=\frac{13.2}{3}=\frac{26}{3}cm\)
Vậy \(BC=13cm;AF=\frac{10}{3}cm;FC=\frac{26}{3}cm\)
giúp mình nốt câu này nhé bạn: mình đã c/m được tam giác ABF đồng dạng được với HBE. c/m tam giác AEF là tam giác cân dùm mình đc không?