Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có: ∠(BAH) +∠(BAD) +∠(DAM) =180o(kề bù)
Mà ∠(BAD) =90o⇒∠(BAH) +∠(DAM) =90o(1)
Trong tam giác vuông AMD, ta có:
∠(AMD) =90o⇒∠(DAM) +∠(ADM) =90o(2)
Từ (1) và (2) suy ra: ∠(BAH) =∠(ADM)
Xét hai tam giác vuông AMD và BHA, ta có:
∠(BAH) =∠(ADM)
AB = AD (gt)
Suy ra: ΔAMD= ΔBHA(cạnh huyền, góc nhọn)
Vậy: AH = DM (hai cạnh tương ứng) (3)
Ta có: ∠(HAC) +∠(CAE) +∠(EAN) =180o(kề bù)
Mà ∠(CAE) =90o⇒∠(HAC) +∠(EAN) =90o (4)
Trong tam giác vuông AHC, ta có:
∠(AHC) =90o⇒∠(HAC) +∠(HCA) =90o (5)
Từ (4) và (5) suy ra: ∠(HCA) =∠(EAN) ̂
Xét hai tam giác vuông AHC và ENA, ta có:
∠(AHC) =∠(ENA) =90o
AC = AE (gt)
∠(HCA) =∠(EAN) ( chứng minh trên)
Suy ra : ΔAHC= ΔENA(cạnh huyền, góc nhọn)
Vậy AH = EN (hai cạnh tương ứng)
Từ (3) và (6) suy ra: DM = EN
Vì DM ⊥ AH và EN ⊥ AH (giả thiết) nên DM // EN (hai đường thẳng cùng vuông góc với đường thẳng thứ ba)
Gọi O là giao điểm của MN và DE
Xét hai tam giác vuông DMO và ENO, ta có:
∠(DMO) =∠(ENO) =90o
DM= EN (chứng minh trên)
∠(MDO) =∠(NEO)(so le trong)
Suy ra : ΔDMO= ΔENO(g.c.g)
Do đó: DO = OE ( hai cạnh tương ứng).
Vậy MN đi qua trung điểm của DE
a)- Ta có: △ABD vuông tại A và \(AB=AD\left(gt\right)\)
=>△ABD vuông cân tại A.
- Ta có: \(\left[{}\begin{matrix}DM\perp AH\left(gt\right)\\BC\perp AH\left(gt\right)\end{matrix}\right.\)=>\(DM\)//\(BC\).
=>\(\widehat{BDM}+\widehat{DMH}=180^0\) (2 góc trong cùng phía).
=>\(\widehat{ADM}+\widehat{ADB}+\widehat{ABH}+\widehat{ABD}=180^0\).
Mà \(\widehat{ADB}=\widehat{ABD}=45^0\)(△ABD vuông cân tại A)
=>\(\widehat{ADM}+45^0+\widehat{ABH}+45^0=180^0\)
=>\(\widehat{ADM}+\widehat{ABH}+90^0=180^0\)
=>\(\widehat{ADM}+\widehat{ABH}=90^0\)
Mà \(\widehat{ADM}+\widehat{MAD}=90^0\) (△ADM vuông tại M).
=>\(\widehat{ABH}=\widehat{MAD}\).
- Xét △ADM vuông tại M và △BAH vuông tại H có:
\(AD=AB\left(gt\right)\)
\(\widehat{ABH}=\widehat{MAD}\) (cmt)
=>△ADM = △BAH (cạnh huyền-góc nhọn).
=>\(DM=AH\) (2 cạnh tương ứng).
b) - Sửa đề: Gọi I là trung điểm của MN.
- Ta có: △ACE vuông tại A và \(AC=AE\left(gt\right)\)
=>△ACE vuông cân tại A.
- Ta có: \(\left[{}\begin{matrix}EN\perp AH\left(gt\right)\\BC\perp AH\left(gt\right)\end{matrix}\right.\)=>\(EN\)//\(BC\).
=>\(\widehat{NEC}+\widehat{HCE}=180^0\) (2 góc trong cùng phía).
=>\(\widehat{AEN}+\widehat{AEC}+\widehat{ACE}+\widehat{ACB}=180^0\).
Mà \(\widehat{AEC}=\widehat{ACE}=45^0\)(△ACE vuông cân tại A)
=>\(\widehat{AEN}+45^0+\widehat{ACB}+45^0=180^0\)
=>\(\widehat{AEN}+\widehat{ACB}+90^0=180^0\)
=>\(\widehat{AEN}+\widehat{ACB}=90^0\)
Mà \(\widehat{AEN}+\widehat{NAE}=90^0\) (△ANE vuông tại N).
=>\(\widehat{ACB}=\widehat{NAE}\).
- Xét △ANE vuông tại N và △CHA vuông tại H có:
\(AN=AC\left(gt\right)\)
\(\widehat{ACB}=\widehat{NAE}\) (cmt)
=>△ANE = △CHA (cạnh huyền-góc nhọn).
=>\(NE=AH\) (2 cạnh tương ứng) mà \(DM=AH\) (cmt)
=>\(NE=DM\).
- Xét △DMI và △ENI có:
\(\left[{}\begin{matrix}DM=NE\left(cmt\right)\\\widehat{DMI}=\widehat{ENI}=90^0\\MI=NI\left(IlàtrungđiểmMN\right)\end{matrix}\right.\)
=>△DMI = △ENI (c-g-c).
=>\(\widehat{DIM}=\widehat{EIN}\) (2 góc tương ứng).
Mà \(\widehat{DIM}+\widehat{DIN}=180^0\) (kề bù).
=>\(\widehat{EIN}+\widehat{DIN}=180^0\)
=>\(\widehat{EID}=180^0\) hay 3 điểm E,I,D thẳng hàng.
Bạn tự vẽ hình nhé!
a, Có ∠BAH+ ∠BAD+ ∠DAM= 180 độ
=> ∠BAH+ ∠DAM= 180 độ- ∠BAD= 90 độ
Xét ΔDAM và ΔABH có
∠ DMA= ∠AHB = 90 độ
AD= AB
∠DAM= ∠ABH (vì cùng phụ với ∠BAH)
=> ΔDAM = ΔABH (ch-gn)
=> DM= AH
b, Có ∠HAC+ ∠EAC+ ∠NAE= 180 độ
=> ∠HAC+ ∠NAE= 180 độ- ∠EAC= 90 độ
Xét ΔEAN và ΔACH có
∠ ANE= ∠AHC = 90 độ
AE= AC
∠NAE= ∠ACH (vì cùng phụ với ∠HAC)
=> ΔEAN = ΔACH (ch-gn)
=> EN= AH
Mà DM= AH
=> EN= DM
c, Có EN ⊥ AH
DM ⊥ AH
=> EN // DM
=> ∠NEO= ∠ODM (2 góc so le trong)
Xét ΔDOM và ΔEON có
∠DMO = ∠ENO = 90 độ
DM= EN
∠ODM= ∠OEN(cmt)
=> ΔDOM = ΔEON (ch-gn)
=> OD = OD
=> O là trung điểm của DE
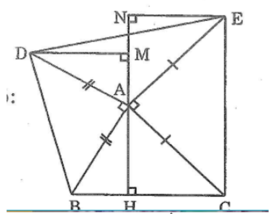
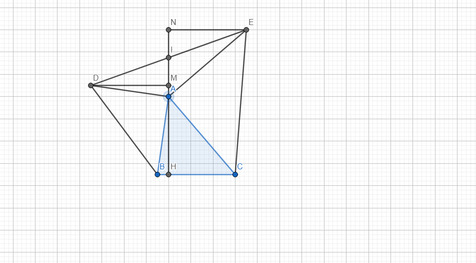
a,Theo hình ta thấy : ^A1 + ^A2 = \(90^o\)(góc \(BAD=90^o\))
mà ^A1+B1=\(90^o\)(tam giác AHB vuông tại H)
-> ^B1 = ^A2
Tam giác vuông ADM = tam giác vuông BAH vì: AB= AD ; ^B1 = ^ A2 (cạnh huyền góc nhọn)
do đó DM = Ah (2 cạnh tương ứng)
b, Tượng tự a -> EN=AH
c, Xét tam giác vuông DOM và tam giác vuông ENO ta có : EN=DM=AH ; ^DOM = ^EON (2 góc đối đỉnh)
nên tam giác vuông DOM = tam giác vuông ENO (cạnh huyền và góc nhọn)
do đó DO + EO ->O là trung điểm DE (đPCM)
Bấm đúng nếu thấy bài viết hữu ích nha!!! :D