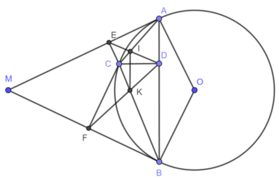
Từ một điểm T ở bên ngoài đường tròn (O), vẽ hai tiếp tuyếnTA; TB với đường tròn (O) (A; B là tiếp điểm). Tia TO cắt đường tròn (O) tại hai điểm phân biệt C và D (C nằm giữa T và O) và cắt đoạn thẳng AB tại điểm F.
1) Cho ∠ADB = 550. Tính ∠TAB; AOB
2) Chứng minh: Tứ giác TAOB nội tiếp
3) Chứng minh TC.TD = TF.TO
4) Chứng minh C là tâm đường tròn nội tiếp DTAB
5*) Vẽ đường kính AG của đường tròn (O). Gọi H là chân đường vuông góc kẻ từ điểm B đến AG, I là giao điểm của TG và BH. Chứng minh I là trung điểm của BH


1: góc ADB=55 độ
góc ADB=góc TAB(=1/2sđ cung AB)
=>góc TAB=55 độ
góc AOB=2*55=110 độ
2:
góc TAO+góc TBO=180 độ
=>TAOB nội tiếp
3: Xét ΔTAC và ΔTDA có
góc TAC=góc TDA
góc ATC chung
=>ΔTAC đồng dạng với ΔTDA
=>TA/TD=TC/TA
=>TA^2=TD*TC
Xét (O) có
TA,TB là tiếp tuyến
=>TA=TB
mà OA=OB
nên OT là trung trực của AB
=>OT vuông góc AB tại F
ΔOAT vuông tại A có AF là đường cao
nên TF*TO=TA^2
=>TF*TO=TC*TD